No mundo da matemática, existem funções, equações de reta, pontos em um plano, figuras geométricas, entre tantos outros casos. Mas como fazer uma representação geométrica desses casos? Para isso, utiliza-se o plano cartesiano. Confira, a seguir, o que é esse sistema de coordenadas, as retas numéricas e os quadrantes, além de videoaulas e exercícios resolvidos sobre o assunto.
Publicidade
O que é plano cartesiano
O filósofo e matemático francês René Descartes desenvolveu a geometria analítica em 1637. Essa nova geometria trazia a possibilidade de fazer uma observação analítica das figuras geométricas. Junto com isso, Descartes desenvolveu o plano cartesiano, pois, com ele, era possível representar todas as figuras em um plano a partir de pontos.
Relacionadas
Entenda, a seguir, os principais conceitos relacionados às aplicações do plano cartesiano.
Retas numéricas
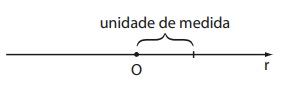
Retas numéricas são retas onde se pode associar, a cada ponto dela, um número real, de tal forma que nenhum desses números seja utilizado duas vezes na reta. Para isso, escolhemos um ponto O chamado origem, uma unidade de medida de comprimento e um sentido positivo (direita).
Coordenadas cartesianas
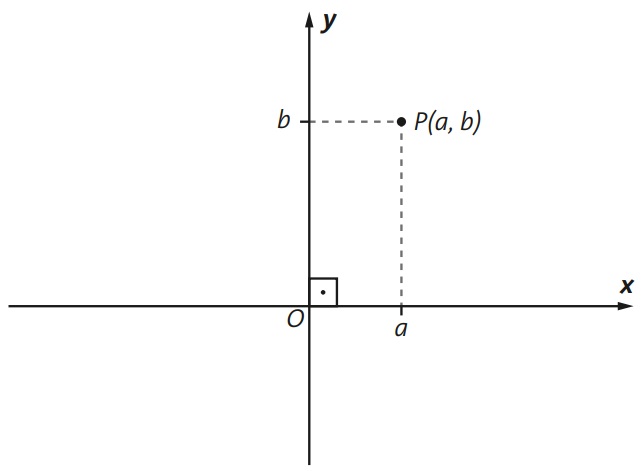
As coordenadas cartesianas são pares ordenados do tipo P (x,y), que são representados no plano cartesiano. Sendo P o ponto, x é o número real que é abcissa de P e y é o número real que é a ordenada de P. Podemos observar essa representação na figura a seguir:
Publicidade
Quadrantes do plano cartesiano
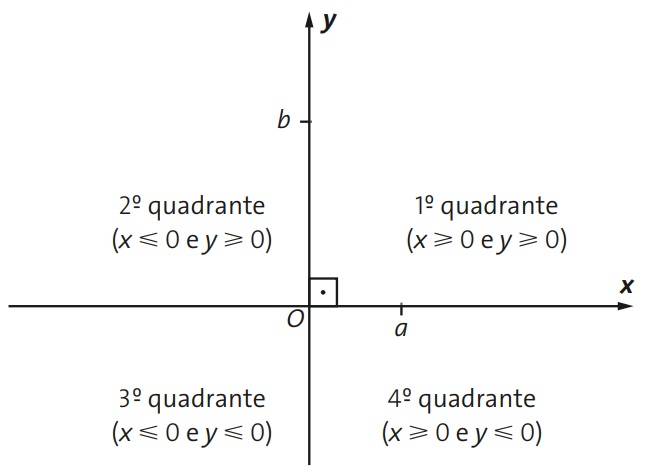
Quando olhamos para o plano cartesiano, vemos uma certa divisão causada pelo cruzamento dos eixos cartesianos. Dessa forma, essa divisão é conhecida como quadrantes. Esses quadrantes são importantes, pois definem o sinal (positivo ou negativo) de cada ponto cartesiano. Como o nome já diz, são 4 divisões que podem ser observadas na figura a seguir.
Publicidade
Na figura, da direita para a esquerda e de cima pra baixo, na ordem, temos: 1° quadrante, 2° quadrante, 3° quadrante e 4° quadrante.
Assim, os sinais para cada quadrante são:
- 1° quadrante: ambas as coordenadas são positivas: x≥0 e y≥0.
- 2° quadrante: a coordenada x é negativa e a y positiva: x≤0 e y≥0.
- 3° quadrante: ambas as coordenadas são negativas: x≤0 e y≤0.
- 4° quadrante: apenas a coordenada y é negativa: x≥0 e y≤0.
Videoaulas sobre plano cartesiano
Nos vídeos a seguir, há várias explicações e aplicações do plano cartesiano, além de uma revisão geral e exercícios resolvidos que vão te ajudar a fixar melhor os conhecimentos aplicados aqui. Confira:
Noções básicas de plano cartesiano
Começamos então com um vídeo que explica as noções básicas de plano cartesiano. Além disso, são apresentados alguns exemplos de pontos cartesianos.
Identificando coordenadas cartesianas
Podemos então agora entender como identificar um ponto cartesiano com o auxílio do vídeo acima.
Uma breve revisão e exercícios resolvidos
Nesse último vídeo, é apresentada uma breve revisão de plano cartesiano, juntamente com a resolução de alguns exercícios sobre esse conteúdo.
Por fim, o plano cartesiano é muito importante na matemática, pois ele dá a base para a geometria analítica. Essa geometria auxilia no entendimento de formas geométricas por meio de um olhar mais analítico. Ou seja, a partir de equações e números, e não mais apenas por figuras ou formas.
Referências
Matemática: ciência e aplicações – ensino médio – Gelson Iezzi [et. al.]
Matemática: contexto & aplicações – ensino médio – Luiz Roberto Dante

Por Guilherme Santana da Silva
Graduado no curso de Física pela Universidade Estadual de Maringá. Professor assistente em um colégio de ensino médio e preparatório para os vestibulares. Nas horas vagas se dedica à vida religiosa, praticar mountain bike, tocar bateria, dar atenção à família e cuidar de suas duas gatinhas Penélope e Mel.
Santana, Guilherme. Plano cartesiano. Todo Estudo. Disponível em: https://www.todoestudo.com.br/matematica/plano-cartesiano. Acesso em: 30 de January de 2026.
1.
Em quais quadrantes estão localizados os pontos:
a) (-2, -4)
b) (3, 1)
c) (0, 6)
d) (8, -7)
e) (9, -3)
a) 3° quadrante
Aqui ambas as coordenadas são negativas.
b) 1° quadrante
Aqui ambas as coordenadas são positivas.
c) 1° quadrante
Igual à anterior
d) 4° quadrante
Aqui só a coordenada y é negativa.
e) 4° quadrante
Igual à anterior.
2.
Qual par ordenado não está representado no plano cartesiano?
a) (3, -4)
b) (4, -3)
c) (-8, -9)
d) (8, 9)
e) (9, -8)

RESPOSTA: e)
Segundo a imagem do exercício, o único ponto que não está presente é o ponto P(9, -8).