No ano de 1637, René Descartes publicou sua obra intitulada como Discurso sobre o método para raciocinar bem e procurar a verdade nas ciências. Essa obra continha um apêndice chamado de Geometria, de muita importância para o mundo científico.
Publicidade
A geometria analítica possibilita o estudo de figuras geométricas a partir de equações e inequações, juntamente com o plano cartesiano, promovendo a união da álgebra com a geometria.
Qual o objetivo da geometria analítica?
René Descartes, um filósofo racionalista, acreditava que a humanidade deveria buscar a verdade por meios dedutivos e não por intuições.
Seguindo essa linha de pensamento, propôs o estudo das figuras geométricas não apenas por desenhos, mas a partir de planos, coordenadas e dos princípios da álgebra e da análise.
Assim, um dos principais objetivos da geometria analítica é desenvolver um pensamento menos abstrato das figuras geométricas, ou seja, um pensamento mais analítico.
Coordenadas
Para iniciarmos os estudos das figuras geométricas, precisamos entender o que são coordenas cartesianas, cilíndricas e esféricas.
Coordenadas cartesianas
Coordenadas cartesianas são coordenadas em um sistema de eixos conhecido como plano cartesiano.
Publicidade
De acordo com sua definição, um plano cartesiano é definido pela intersecção do eixo x (abscissa) com o eixo y (ordenada) formando um ângulo de 90° entre eles.
O centro desse plano é chamado de origem e pode ser representado pela letra O, conforme a figura a seguir.
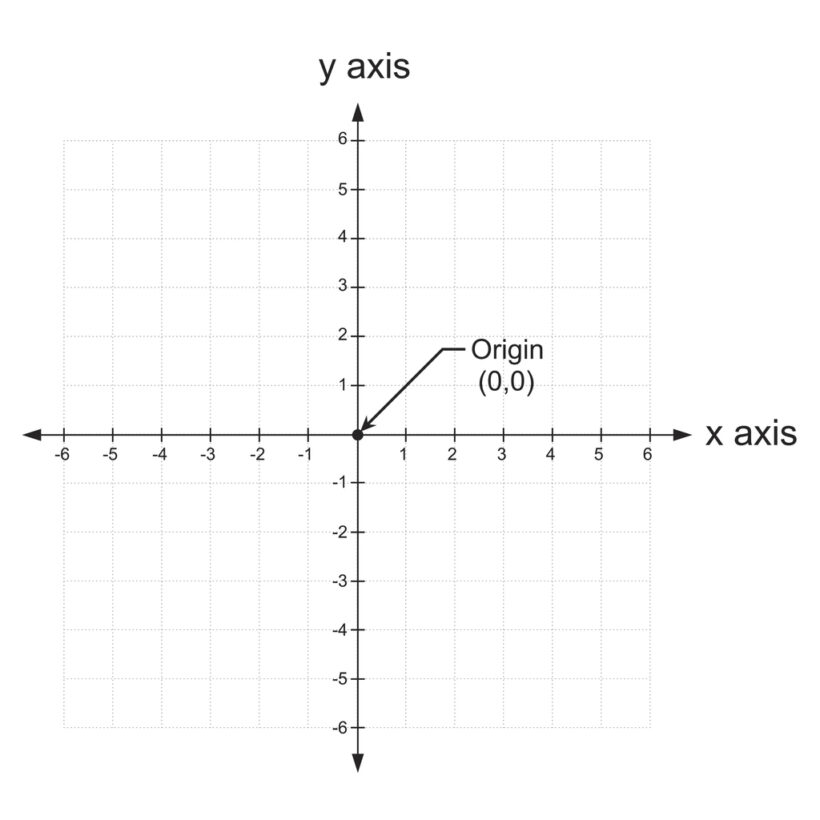
Com isso, podemos definir um ponto P que contém dois números a e b, sendo respectivamente, a projeção do ponto P no eixo x e no eixo y.
Publicidade
Assim, um ponto no plano cartesiano seria P(a,b) ou, de uma forma genérica, P(x,y).
Existem ainda outros tipos de coordenadas, como as cilíndricas e as esféricas que, por serem mais complexas, são estudadas no Ensino Superior.
Curvas e equações
De acordo com as noções obtidas até o momento, vamos entender um pouco melhor a aplicação da Geometria Analítica às diferentes formas geométricas.
Equações da reta em um plano cartesiano
A princípio, toda reta do plano cartesiano pode ser representada por três diferentes equações: geral, reduzida e paramétrica.
A equação geral da reta é definida da seguinte maneira:
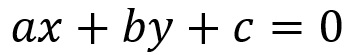
De acordo com a equação geral da reta, temos que x e y são variáveis e a, b e c são constantes.
Sob o mesmo ponto de vista, a equação reduzida da reta é definida como se segue:
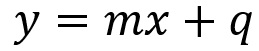
Só para exemplificar, temos que m é o coeficiente angular da reta e q é o coeficiente linear.
Por fim, a equação paramétrica da reta são equações que, de certa forma, relacionam apenas as variáveis x e y, podendo essas variáveis serem em função de um parâmetro t.
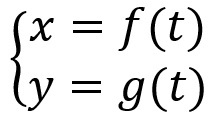
Equações da circunferência
Da mesma forma que a reta, uma circunferência também pode ser representada por mais de uma equação. Tais equações são a equação reduzida e a equação normal.
Em primeiro lugar, a equação reduzida da circunferência pode ser definida da seguinte forma:
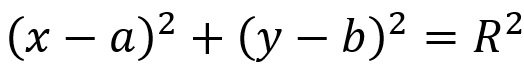
Segundo essa equação, as constantes a e b representam o centro C da circunferência, ou seja, C(a,b). Sob o mesmo ponto de vista, a constante R representa o raio dessa circunferência.
Em segundo lugar vem a equação normal. Ela pode ser definida da seguinte forma:
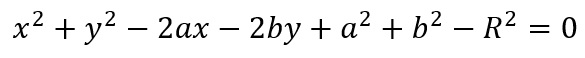
Em suma, os elementos da equação normal são os mesmo da equação reduzida.
Aplicações da geometria analítica no cotidiano
Vamos aprofundar um pouco mais nossos estudos com os vídeos a seguir.
Equação geral da reta
O vídeo demonstra como obter a equação geral da reta e um macete para memorizá-la.
Exercício resolvido
Esse vídeo nos ajuda a entender um exercício sobre equação reduzida da reta com uma explicação passo a passo.
Equação normal da circunferência
Esse último vídeo explica como se obter a equação normal da circunferência, juntamente com um macete para lembrar dessa equação.
Por fim, a geometria analítica fez com que a matemática desse um salto imenso em suas áreas. Por isso é tão importante estuda-lá.
Referências
Luiz Roberto Dante, Matemática: contexto & aplicações: ensino médio;
Manoel Paiva, Matemática.

Por Guilherme Santana da Silva
Graduado no curso de Física pela Universidade Estadual de Maringá. Professor assistente em um colégio de ensino médio e preparatório para os vestibulares. Nas horas vagas se dedica à vida religiosa, praticar mountain bike, tocar bateria, dar atenção à família e cuidar de suas duas gatinhas Penélope e Mel.
Santana, Guilherme. Geometria analítica. Todo Estudo. Disponível em: https://www.todoestudo.com.br/matematica/geometria-analitica. Acesso em: 07 de February de 2026.
1. [FUVEST-SP]
Se (m+2n , m – 4) e (2 – m , 2n) representam o mesmo ponto do plano cartesiano, então mn é igual a:
a) –2
b) 0
c) √2
d) 1
e) 1/2
Se (m+2n, m-4) e (2-m, 2n) representam o mesmo ponto no plano, então suas coordenas são iguais. Assim,
m + 2n = 2 – m
Agrupando m e n, temos
m + m + 2n = 2;
2m + 2n = 2 (1)
Além disso,
m – 4 = 2n;
m – 2n = 4 (2)
Temos então o seguinte sistema,
2m + 2n = 2
m – 2n = 4
Resolvendo o sistema, obtemos que m = 2 e n = -1
Dessa forma:
mn = (2)-1
A resposta correta é a letra e.
2. [PUC-SP]
O ponto P(3, b) pertence à circunferência de centro no ponto C(0, 3) e raio 5. Calcule valor da coordenada b.
Temos por (x – a)² + (y – b)² = r², que a circunferência de centro C(0 ,3) e raio 5, possui como representação a equação (x – 0)² + (y – 3)² = 5² ou x² + (y – 3)² = 25.
Considerando que o ponto P(3, b) pertença à circunferência, então:
x² + (y – 3)² = 25
3² + (b – 3)² = 25
9 + (b – 3)² = 25
(b – 3)² = 25 – 9
(b – 3)² = 16
b – 3 = 4 ou b – 3 = – 4
b = 4 + 3 ou b = –4 + 3
b = 7 ou b = –1
A coordenada b pode assumir os valores 7 ou –1.