O conceito de função está presente em nosso cotidiano desde a antiguidade. Claudio Ptolomeu utilizou esse conceito em sua época, mas o nome função apareceu apenas em 1698 com os matemáticos Jean Bernoulli e Gottfried Leibniz. Para eles, uma função é “… uma quantidade que de alguma maneira é formada por quantidades indeterminadas e quantidades constantes”. Vamos então estudar alguns conceitos e definição de funções.
Publicidade
O que são funções?
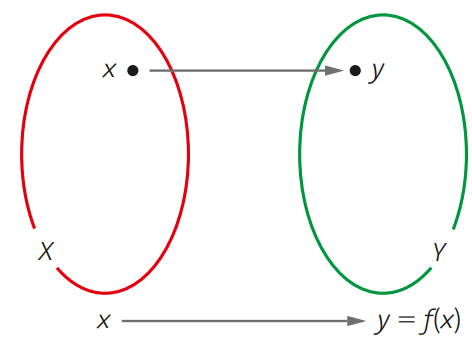
Podemos definir uma função, de uma forma simples, como sendo a relação entre duas grandezas variáveis. Mas, conforme houve uma evolução na matemática e com o desenvolvimento do diagrama de Venn, podemos também definir uma função como na imagem a seguir e na definição formal de uma função:
Relacionadas
Dados os conjuntos X e Y, uma função f: X → Y (lê-se: uma função de X em Y) é uma regra que determina como associar a cada elemento x∈X um único y = f(x)∈Y.
Essa é uma definição padrão e primordial de funções, porém existem muitos tipos diferentes de funções com suas características e definições individuais.
Quando não é uma função
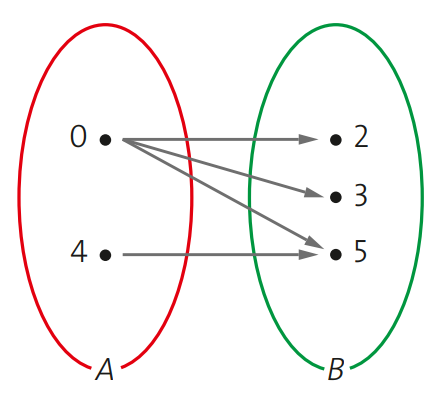
Algumas relações não são consideradas funções. Vamos ver alguns exemplos sobre isso. Na figura a seguir temos uma relação do conjunto A com o B.
Publicidade
Essa relação não é uma função pois temos que um único elemento do conjunto A se relaciona com vários elementos do conjunto B, violando assim a definição de função.
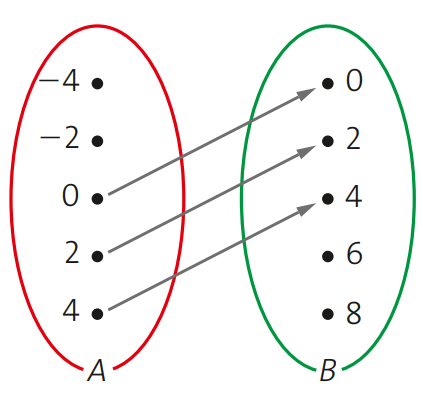
Outro exemplo de uma não função é apresentado a seguir:
Publicidade
Existem elementos em A que não se relacionam com elementos do conjunto B, violando também a definição de função.
Isso nos ajuda a identificar o que seria ou não uma função olhando apenas para seu domínio e contradomínio.
Tipos de funções
Como já mencionado, existem vários tipos de funções na matemática. Vamos abordar, de uma forma curta e objetiva, alguns desse tipos.
Função afim
![]()
Essa função é conhecida também como função do primeiro grau e é muito utilizada na física e na química. O gráfico dessa função é uma reta.
Função quadrática
![]()
Muitas vezes conhecida como função do segundo grau, aparece muito na geometria e em algumas situações físicas como o movimento retilíneo uniformemente variado. É uma parábola que caracteriza o gráfico dessa função.
Função exponencial
![]()
Em certas situações, como por exemplo uma população de bactérias, uma função afim não consegue descrever o fenômeno, pois a população cresce muito rápido. Dessa forma é necessário utilizar a função exponencial.
Além dessas funções, existem também as funções trigonométricas e a logarítmica. Algumas dessas funções já foram abordadas e conceituadas em outros texto aqui do site.
Videoaulas
Selecionamos as melhores videoaulas do Youtube para te auxiliar com os estudos. Dessa forma, vamos abordar o conteúdo de funções a partir de vídeos didáticos.
Noções básicas
Aqui é possível compreender um pouco mais sobre as definições de uma função e alguns exemplos.
Identificando funções
Sabemos que algumas relações não são funções, esse vídeo mostra como identificar se tal relação é função ou não
Entender o conceito de função nos ajuda a compreender todos os outros tipos de funções que são abordadas no mundo da matemática.
Referências
Matemática: ciência e aplicações: ensino médio – Gelson Iezzi. . . [et. al.];
Matemática: contexto & aplicações: ensino médio – Luiz Roberto Dante.

Por Guilherme Santana da Silva
Graduado no curso de Física pela Universidade Estadual de Maringá. Professor assistente em um colégio de ensino médio e preparatório para os vestibulares. Nas horas vagas se dedica à vida religiosa, praticar mountain bike, tocar bateria, dar atenção à família e cuidar de suas duas gatinhas Penélope e Mel.
Santana, Guilherme. Funções. Todo Estudo. Disponível em: https://www.todoestudo.com.br/matematica/funcoes. Acesso em: 03 de February de 2026.
1.
Dados os conjuntos A={a,b,c} e B={1,2,3,4}, podemos construir a relação R em A×B que está apresentada no gráfico.
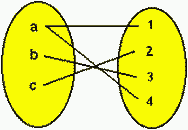
a. R={(a,1),(b,3),(c,4),(a,3)}
b. R={(1,a),(4,a),(3,b),(c,2)}
c. R={(a,1),(b,3),(c,2)} d. R={(a,1),(a,4),(b,3),(c,2)}
(a) Não, pois a relação deve conter (c,2) e (a,4).
(b) Não, pois os elementos da esquerda devem estar relacionados com os da direita, e não o contrário.
(c) Não, pois falta o par ordenado (a,4).
(d) Resposta correta.
2.
Quais dos diagramas melhor se encaixa na definição de uma função de A em B, onde A={a,b,c} e B={1,2,3}.
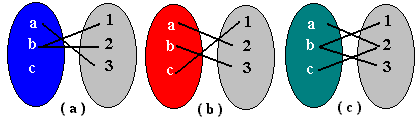
A alternativa a) não pode ser pois um elemento do primeiro conjunto se relaciona duas vezes com elementos distintos do segundo conjunto.
O mesmo ocorre para a alternativa c).
Portanto, a alternativa correta é a b) pois ela não viola a definição de função.