Função afim ou função polinomial do 1° grau é toda função que estabelece uma relação entre a variável dependente y e a variável independente x. Em outras palavras, essa relação tem uma parte fixa e outra variável, que depende do valor da variável independente. A seguir, confira definição, gráfico e fórmula, além de exemplos e exercícios resolvidos sobre o assunto.
Publicidade
Definição
Uma função afim pode ser definida formalmente da seguinte maneira:
Relacionadas
Chama-se função polinomial do 1° grau, ou função afim, qualquer
função f de R em R dada por uma lei da forma f(x) = ax + b, em que a e b são números reais dados e a≠0.
Fórmula
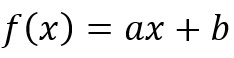
Na função afim, o número a é chamado de coeficiente angular e b é conhecido como coeficiente linear.
Características da função afim
- Crescente: uma função afim é crescente quando seu coeficiente angular for positivo, ou seja, a > 0.
- Decrescente: por outro lado, a função afim é considerada decrescente quando o coeficiente angular é negativo, ou seja, a < 0.
Gráfico de uma função afim
Assim como muitas outras, a função afim também possui um gráfico específico. Dessa forma, vamos entender um pouco mais sobre esse gráfico e observar como ele é representado.
Publicidade
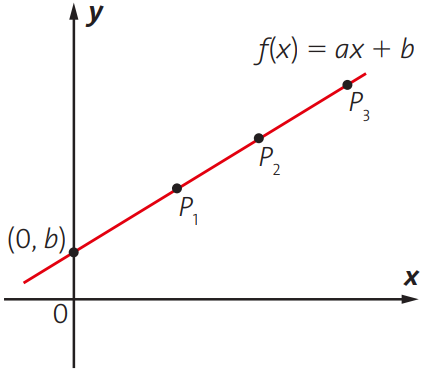
O gráfico dessa função é uma reta. O coeficiente linear b é, geometricamente falando, o ponto que intersecta o eixo das ordenadas (eixo y). Já o coeficiente angular a é a taxa de variação que essa reta tem em relação ao eixo das abcissas (eixo x).
Tipos de função afim
Para algumas situações, podemos obter alguns tipos diferentes de função afim. Sendo assim, vamos compreender cada situação que possamos encontrar.
Publicidade
Função linear
![]()
A função linear ocorre quando o coeficiente linear é igual a zero. Dessa forma, os elementos y e x são grandezas diretamente proporcionais entre si.
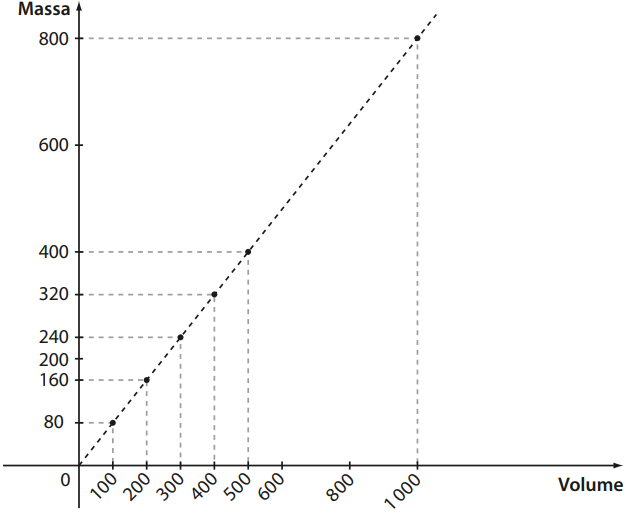
O gráfico acima representa um exemplo de função linear em que a massa e o volume de um determinado azeite variam proporcionalmente.
Função identidade
![]()
Quando temos que a=1 e b=0, a função afim se torna uma função identidade, ou seja, temos que y = x.
Função constante
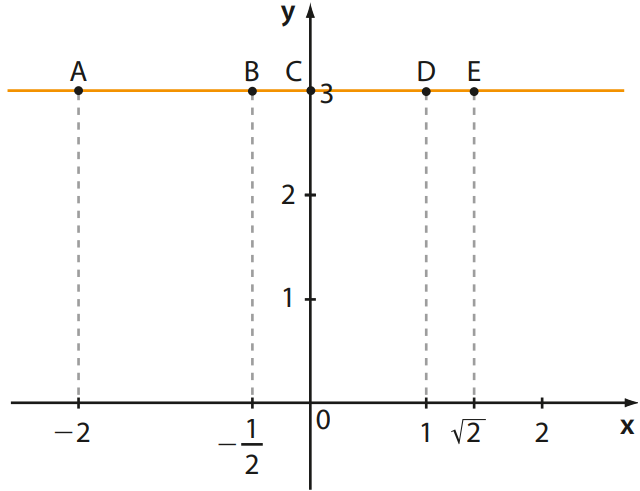
Se tivermos que a=0 e b≠0, a função afim se torna uma função constante. Um exemplo disso pode ser visto no gráfico a seguir, onde temos que f(x) = 3.
Raiz da função afim
A raiz de uma função ocorre quando f(x) = 0, ou seja, é o valor de x que faz com que essa função se anule. Para a função afim, temos que ax + b = 0. Resolvendo essa equação, obtemos que a raiz de uma função afim:
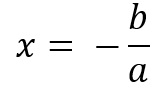
Videoaulas sobre função afim
Abaixo, foram selecionados os melhores vídeos com explicações sobre função afim que podem ajudar a visualizar melhor o conteúdo. Acompanhe:
Conceitos iniciais
Nesse vídeo, são abordados os conceitos iniciais de função afim, como sua definição. Além disso, são apresentados alguns exemplos.
Exercícios resolvidos
Resolver exercícios também é uma maneira de entender o conteúdo. Dessa forma, que tal conferir alguns exercícios resolvidos a partir do vídeo acima?
Função afim crescente e decrescente
Vamos entender também como reconhecer se uma função afim é crescente ou decrescente com a ajuda do vídeo acima. Acompanhe!
Por fim, é importante lembrar que a função afim, assim como as outras, é muito importante para os estudos de matemática, pois é possível descrever várias situações utilizando-a. Além disso, há aplicações também na física, como no movimento retilíneo e uniforme.
Referências
Matemática: ciência e aplicações, volume 1 – Gelson Iezzi
Matemática: contexto e aplicações, volume 1 – Luiz Roberto Dante

Por Guilherme Santana da Silva
Graduado no curso de Física pela Universidade Estadual de Maringá. Professor assistente em um colégio de ensino médio e preparatório para os vestibulares. Nas horas vagas se dedica à vida religiosa, praticar mountain bike, tocar bateria, dar atenção à família e cuidar de suas duas gatinhas Penélope e Mel.
Santana, Guilherme. Função afim. Todo Estudo. Disponível em: https://www.todoestudo.com.br/matematica/funcao-afim. Acesso em: 20 de February de 2026.
1. [UFPI]
A função real de variável real, definida por f (x) = (3 – 2a).x + 2, é crescente quando:
a) a > 0
b) a 3/2
e) a < 3
RESPOSTA: b)
Para que a função seja crescente, o coeficiente de x deve ser positivo. Assim:
3 – 2a > 0
Multiplicando ambos os lados por -1, temos que:
-3 + 2a < 0
Somando 3 em ambos os lados, obtemos:
2a < 3
Por fim, dividindo ambos os lados por 2, temos:
a < 3/2
2. [FGV]
O gráfico da função f (x) = mx + n passa pelos pontos (– 1, 3) e (2, 7). O valor de m é:
a) 5/3
b) 4/3
c) 1
d) 3/4
e) 3/5
RESPOSTA: b)
O primeiro ponto que é dado é o (– 1, 3), em que o valor de x é – 1 e o valor de f(x) é 3. Substituindo esses valores na função, temos:
f(x) = mx + n
3 = m.(– 1) + n
n = 3 + m
Vamos também substituir o segundo ponto (2, 7) na função, sendo que x vale 2 e f(x) vale 7:
f(x) = mx + n
7 = m.2 + n
n = 7 – 2m
Nas duas substituições feitas, encontramos dois valores para n. Se igualarmos essas duas equações, teremos:
3 + m = 7 – 2m
m + 2m = 7 – 3
3m = 4
m = 4/3