Uma função pode ser definida de várias formas, dependendo de como o seu conjunto domínio se relaciona com o conjunto do contradomínio. Assim, podemos encontrar uma função injetora, sobrejetora ou bijetora.
Publicidade
Dessa forma, iremos estudar um pouco mais sobre a função sobrejetora. Conheceremos então o domínio e o contra domínio dessa função, além de observamos o gráfico, alguns exemplos e resolver exercícios.
O que é uma função sobrejetora
Primeiramente, vamos entender um pouco mais sobre o que é um domínio e um contradomínio de uma função.
O domínio de uma função é o conjunto de “origem”, ou seja, é o conjunto que define a função. Por sua vez, o contradomínio é o conjunto de “destino”, assim, é o conjunto que contém todas as possíveis imagens da função.
Relacionadas
Seja f uma função qualquer. Se o conjunto A for seu domínio e B o seu contradomínio, f será sobrejetora quando todo elemento de B for imagem de pelo menos um elemento do conjunto A, ou seja, todo elemento do conjunto B é imagem do conjunto A.
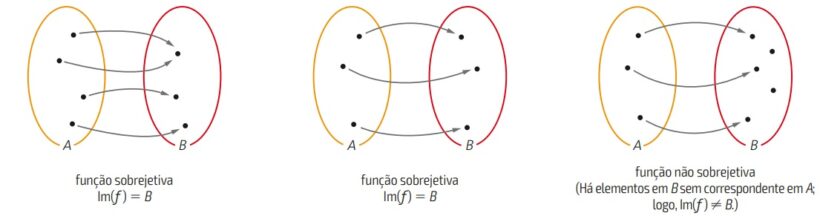
A partir da imagem anterior, podemos então analisar quais as relações de domínio e de contradomínio que se encaixam na definição de função sobrejetora. Nas duas primeiras relações temos uma função sobrejetora, pois todos os elementos do contradomínio se relacionam com pelo menos um elemento do domínio. Porém, na última relação isso não acontece.
De uma maneira mais formal, a função sobrejetora pode ser definida da seguinte forma:
Publicidade
Uma função f:A→B é sobrejetora, quando para qualquer elemento y∈B, pode-se encontrar um elemento x∈A tal que f(x)=y.
Exemplos de função sobrejetora
Conforme o que foi visto até aqui, é possível identificar alguns exemplos de funções sobrejetora.
Uma função linear simples
Seja f(x) = x + 2. Essa função é sobrejetora, pois todo elemento do conjunto dos números reais é imagem de um elemento do contradomínio também dos números reais. Veja:
Publicidade
- f(x) = 5 é imagem de x = 3, pois 5 – 2 = 3;
- f(x) = 0 é imagem de x = -2, pois 0 – 2 = -2.
A função quadrática
Uma função muito conhecida, a função f(x) = x2 definida como f: R → R+, também é sobrejetora, pois todos os elementos do contradomínio de f(x) são imagem de pelo menos um elemento do domínio de f(x). Observe:
- f(x) = 9 é imagem de 3 e -3.
- f(x) = 4 é imagem de 2 e -2.
Existem muitas outras funções que são sobrejetoras. Tais exemplos apresentados foram apenas para haver um entendimento melhor do que foi estudado.
Gráfico de uma função sobrejetora
Podemos saber se uma função é sobrejetora ou não apenas analisando seu gráfico. Para isso, basta apenas observarmos se no gráfico sobram valores no contradomínio da função. Então, analisaremos o seguinte gráfico:
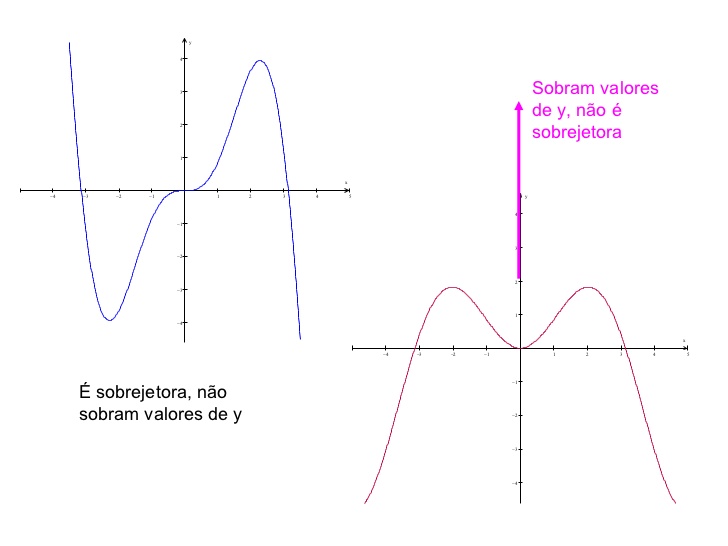
Segundo a imagem anterior, o gráfico da esquerda representa uma função sobrejetora, pois todos os valores do contradomínio estão relacionados com algum elemento do domínio. Por outro lado, o segundo gráfico não é uma função sobrejetora, pois “sobram” valores em seu contradomínio.
Essa é um método que facilita muito a identificação de uma função sobrejetora. Em alguns exercícios, isso é importante, economizando tempo e recursos para a resolução.
Entenda mais sobre função sobrejetora
Muitos são os recursos hoje em dia para se ter conhecimento sobre um determinado assunto. Além do texto apresentado, podemos aprender um pouco mais sobre as funções sobrejetora a partir dos vídeos abaixo.
Definição e exemplos de função sobrejetora
Neste vídeo, é abordado a definição de uma função sobrejetora, junto com as devidas explicações, e alguns exemplos dessa função.
Definições e exercícios resolvidos
Por outro lado, esse vídeo aborda, além da definição de função sobrejetora, exercícios resolvidos de muitos vestibulares do Brasil.
Os vídeos são uma ferramenta muito importante para o aprofundamento de um determinado assunto. No nosso estudo sobre função sobrejetora também não poderia ser diferente.
Referências
Matemática: ciência e aplicações – Gelson Iezzi;
Matemática: contexto & aplicações – Luiz Roberto Dante.

Por Guilherme Santana da Silva
Graduado no curso de Física pela Universidade Estadual de Maringá. Professor assistente em um colégio de ensino médio e preparatório para os vestibulares. Nas horas vagas se dedica à vida religiosa, praticar mountain bike, tocar bateria, dar atenção à família e cuidar de suas duas gatinhas Penélope e Mel.
Santana, Guilherme. Função sobrejetora. Todo Estudo. Disponível em: https://www.todoestudo.com.br/matematica/funcao-sobrejetora. Acesso em: 20 de February de 2026.
1.
A respeito da definição de funções sobrejetoras, assinale a alternativa correta:
a) Uma função é sobrejetora quando cada elemento do contradomínio está relacionado a um único elemento do domínio.
b) Em um diagrama de uma função sobrejetora, não pode haver duas flechas com extremidades no mesmo ponto do contradomínio.
c) Toda função é sobrejetora.
d) Toda função injetora é sobrejetora.
e) Uma função é sobrejetora quando o contradomínio e a imagem são iguais.
a) Incorreta!
Essa é a definição de função injetora.
b) Incorreta!
Esse é o diagrama de uma função injetora.
c) Incorreta!
Se toda função fosse sobrejetora, não haveria necessidade dessa classificação. Nem toda função é sobrejetora. Por exemplo, a função f(x) = x2 não é sobrejetora porque seu contradomínio e imagem não coincidem.
d) Incorreta!
Qualquer função pode ser injetora e ainda possuir contradomínio diferente da imagem. Portanto, nem toda função injetora é sobrejetora.
e) Correta!
RESPOSTA: e)
2.
Determine o valor de b em B = {y∈R/y≥b} de modo que a função f de R definida em B por f(x) = x2 – 4x + 6 seja sobrejetora
Para que a função seja sobrejetora, precisamos que a imagem seja igual ao contradomínio.
O vértice da função f(x) ocorre no ponto (2,2) de um plano cartesiano. Assim, o domínio de f(x) só atingirá valores maiores do que 2 no contradomínio.
Portanto, isso significa que para a imagem ser igual ao contradomínio, o nosso b precisa ser maior ou igual a 2.