Função exponencial

A função exponencial tem várias aplicações, não somente na matemática. Temos a lei de resfriamento na física e o decaimento radioativo na química, por exemplo. Além disso, a biologia e a geografia buscam, na função exponencial, explicar crescimentos ecológicos e sociológicos. Alguns desses casos vão apresentar um crescimento ou decaimento, o que será visto mais adiante.

Publicidade

Mas como representar matematicamente uma função exponencial? Vamos supor que, em uma determinada cultura de bactéria, a população dobre seu valor a cada hora. No início existiam 1000 bactérias. Quando se passou 3 horas, percebeu-se que haviam 8000 bactérias e, passado 10 horas do início do experimento, constatou-se que haviam 10240000. Se passar x horas, quantas bactérias existirão no experimento? A resposta dessa pergunta se dá pela definição de uma função exponencial:

Dado um número real a (a > 0 e a ≠ 1), denomina-se função exponencial de base a uma função f: |R→ |R*+ é definida por f(x)=a^x

Exemplos de função exponencial

Com a definição padrão da função exponencial em mente, vamos agora para alguns exemplos.

Exemplo 1

Vamos tomar o exemplo citado acima sobre a colônia de bactérias. Neste caso, teríamos a função exponencial f(x) = b∙2^x, sendo b a quantidade de bactérias no início do experimento que, no caso do nosso exemplo, seria de 1000 bactérias.

Exemplo 2

Um outro exemplo bem interessante: suponha que a dívida inicial de uma certa cidade seja de 1 milhão de reais, ou seja x = 0. A partir de agora, a dívida começa a dobrar em relação ao valor devido uma década anterior. Teremos então a seguinte função exponencial para esse exemplo f(x) = 2^x.

Publicidade

Exemplo 3

Agora um exemplo de função exponencial para a física. Quando um elemento é radioativo, ou seja, emite radiação, ele tem um tempo de meia-vida que é o tempo que demora para que a metade dos átomos radioativos desse elemento se desintegre. Isso é representado pela função exponencial f(x) = n0∙e^-c∙x, onde x é o tempo decorrido do início da radiação, n0 é o número inicial de elementos radioativos e c é a constante de decaimento.

Como diferenciar uma função exponencial que cresce ou decresce? Ou, ainda, o que seria uma função exponencial crescente ou decrescente? Para responder essas perguntas, precisamos entender quais são os tipos de funções.

Tipos de função exponencial

Nos dois primeiros exemplos, pode-se observar que a quantidade da colônia de bactérias e a dívida da cidade aumentavam conforme o tempo ia passando. Já no terceiro exemplo, acontecia o contrário. Identifiquemos então quando uma função exponencial é crescente ou decrescente.

Publicidade

Crescente

Como nos dois primeiros exemplos, se algo cresce de forma muito rápida, mas com um certo padrão, então tal coisa cresce exponencialmente. Uma função é crescente quando:

a > 1

Decrescente

Se em uma determinada situação existe uma queda muito grande, só que de uma forma padronizada, então dizemos que ela cai exponencialmente. Uma função é decrescente quando:

0 < a < 1, ou seja, quando a está entre os valores 0 e 1 (não sendo permitido ser igual a tais valores).

Gráfico da função exponencial

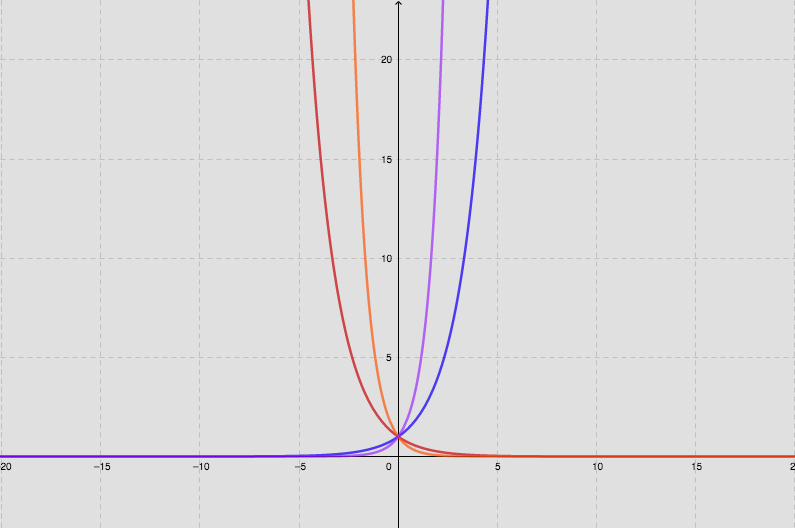
Podemos observar as seguintes características na Figura 1:

Os gráficos em cores azul e roxo são gráficos de funções exponenciais crescentes, pois tem-se que a > 1.

Já nos gráficos nas cores laranja e vermelho, observa-se funções exponenciais decrescentes, pois 0 < a < 1.

Função exponencial: resumo

No vídeo abaixo, podemos ver um breve resumo sobre as funções exponenciais e seus tipos crescente e decrescente.

Referências