Espelhos curvos podem apresentar diversos perfis. O perfil de interesse de estudo aqui é o espelho esférico formado a partir de um arco de circunferência ou de uma calota esférica espelhada. Veremos também os elementos geométricos de um espelho esférico, os dois tipos de espelhos esféricos, o referencial de Gauss e as equações desses espelhos.
Publicidade
Elementos geométricos
Antes de mais nada, vamos começar estudando a respeito dos elementos que fazer parte de um espelho esférico. A imagem a seguir mostra quais são eles.
Relacionadas
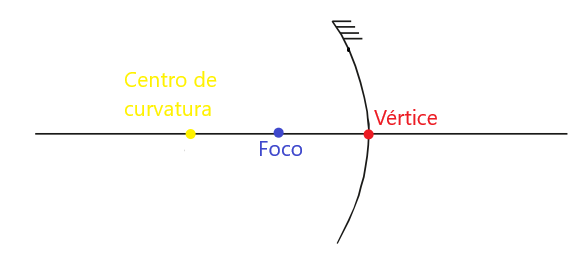
Assim, podemos descrever cada um desses elementos a seguir.
Vértice
É conhecido como o centro geométrico de um espelho esférico. Todo raio de luz que incide sobre o vértice é refletido com o mesmo ângulo de incidência, do mesmo modo que em um espelho plano.
Centro de curvatura
É o centro da superfície esférica que deu origem ao espelho. Em outras palavras, o centro de curvatura é o raio dessa esfera. Todo raio de luz que incide sobre o centro de curvatura é refletido de volta pelo mesmo caminho, ou seja, ele é refletido no centro de curvatura. É chamado de raio de curvatura a distância entre o vértice do espelho esférico e seu centro de curvatura.
Publicidade
Além disso, o eixo que passa entre o vértice o centro de curvatura é chamado de eixo principal de um espelho esférico.
Foco
Ponto que fica exatamente na metade da distância entre o centro de curvatura e o vértice. Essa distância é chamada de distância focal. Além disso, todo raio de luz paralelo ao eixo principal que incide no espelho côncavo converge para o foco, nesse caso sendo um foco real. No caso de um espelho convexo, o raio de luz diverge sendo o prolongamento desses raios que se encontram em um ponto atrás do espelho, chamado de foco virtual.
Estudaremos ainda nesta matéria sobre os espelhos esféricos côncavo e convexo.
Publicidade
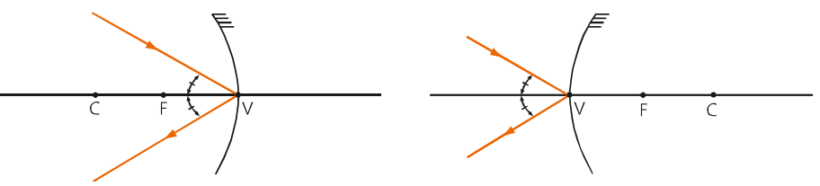
Angulo de abertura (α)
É o ângulo formado pelos raios que passam pelos pontos extremos A e B, simétricos em relação ao eixo principal. Quanto maior for esse ângulo, mais um espelho esférico se parece com um espelho plano.
Espelhos côncavos
Podemos ver uma ilustração de um espelho esférico côncavo na imagem a seguir.
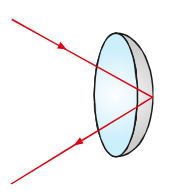
Em outras palavras, um espelho esférico é considerado côncavo quando a parte interna da calota do espelho for refletora, conforme vemos na imagem anterior. Dessa forma, vamos estudar como as imagens são formadas nesse tipo de espelho.
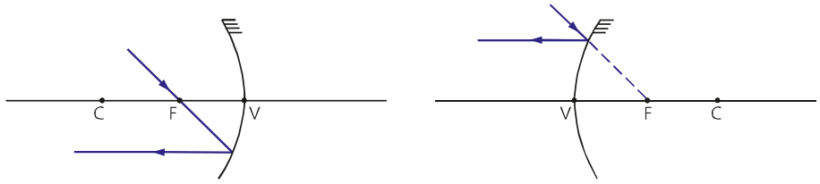
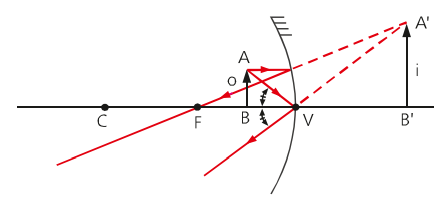
Objeto entre o vértice e o foco
Quando um objeto é colocado entre o foco e o vértice do espelho, a imagem gerada é virtual, direita e menor. Chamamos uma imagem de virtual quando é utilizado o prolongamento dos raios incidentes para criar a imagem.
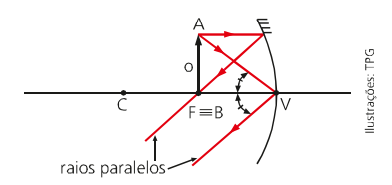
Objeto sobre o foco
É impossível gerar uma imagem quando colocamos um objeto no foco de um espelho côncavo. Chamamos isso de imagem imprópria, pois os raios incidentes só se “cruzam” no infinito, e assim criando uma imagem apenas no infinito.
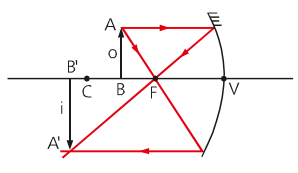
Objeto entre o centro de curvatura e o foco
A imagem formada por um espelho côncavo, quando o objeto está entre o centro de curvatura e o foco, é uma imagem real, invertida e maior que o objeto.
Consideramos que uma imagem é real quando os raios refletidos se “cruzam”, formando a imagem. Uma imagem invertida, de certa forma, é uma imagem que possui o sentido oposto do objeto. Em outras palavras, se o objeto está para cima, a imagem estará para baixo e vice-versa.
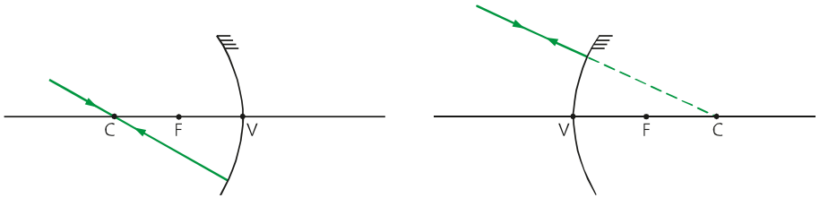
Objeto sobre o centro de curvatura
Para um objeto sobre o centro de curvatura de um espelho côncavo, a imagem formada é real, invertida e igual ao tamanho do objeto.
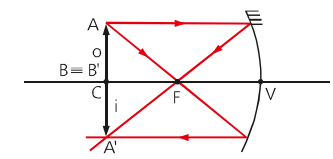
Objeto a esquerda do centro de curvatura
Neste último caso de formação de imagem em um espelho côncavo, onde o objeto está a esquerda do centro de curvatura, a imagem formada é real, invertida e menor.
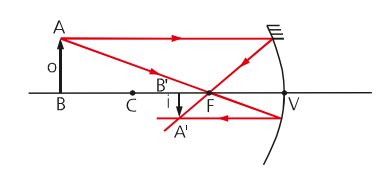
Espelhos convexos
Um espelho esférico é chamado de convexo quando a parte externa de uma calota esférica é refletora. Uma ilustração disso pode ser observada a seguir.
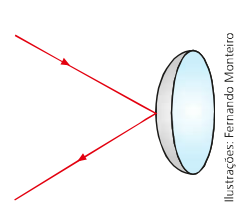
Independente de onde colocamos o objeto nesse tipo de espelho a imagem sempre será a mesma. Em outras palavras a imagem será virtual, direita e menor que o objeto.
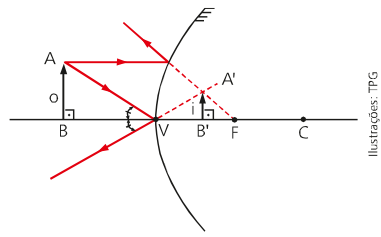
Referencial de Gauss
Para o estudo analítico (matemático) precisamos entender o que é o referencial de Gauss. Ele é muito parecido com o plano cartesiano matemático, porém com diferenças nas convenções dos sinais para os eixos ordenados. Dessa forma, vamos entender esse referencial a partir da imagem a seguir.
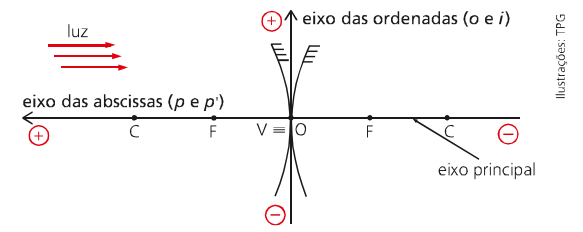
- O eixo das abscissas é chamado de abscissa do objeto/imagem;
- Para os eixos das ordenadas é dado o nome de ordenada do objeto/imagem;
- No eixo das abscissas é convencionado que o sinal positivo fique a esquerda e no eixo das ordenadas para cima;
- Matematicamente os pares ordenados para o objeto serão A=(p; o) e para a imagem A’=(p’;i).
Fórmulas e equações
Com o referencial de Gauss em mente, vamos analisar as duas equações que regem o estudo analítico dos espelhos esféricos.
Equação de Gauss
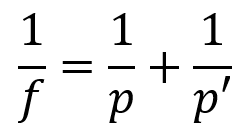
- f: distância focal
- p: distância do objeto até o vértice do espelho
- p’: é a distância da imagem até o vértice do espelho.
Essa equação é a relação entre a distância focal com as abscissas do objeto e da imagem. Ela também é conhecida como equação dos pontos conjugados.
Aumento linear transversal
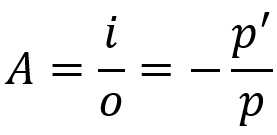
- A: aumento linear;
- o: tamanho do objeto;
- i: tamanho da imagem;
- p: distância do objeto até o vértice do espelho;
- p’: distância entre o vértice do espelho e a imagem.
Essa relação nos diz qual é o tamanho da imagem em relação ao objeto. O sinal negativo na equação é referente a uma ordenada negativa no referencial de Gauss.
Videoaulas sobre espelhos esféricos
Para não ficar nenhuma duvida para trás, apresentamos agora alguns vídeos a respeito do conteúdo estudado até aqui.
O que são espelhos côncavos e convexos
Entenda nesse vídeo alguns conceitos básicos sobre os dois tipos de espelhos esféricos. Assim, todas as dúvidas sobre eles podem ser sanadas!
Formação de imagens
Para que nenhuma dúvida sobre a formação de imagens nos espelhos esféricos fique para trás, apresentamos aqui esse vídeo que explica sobre o assunto.
Aplicação das equações de espelhos esféricos
É importante entender sobre as equações apresentadas para você arrasar nas provas. Pensando nisso, o vídeo acima apresenta um exercício resolvido onde são aplicadas as equações dos espelhos esféricos. Confira!
Outro assunto importante para se entender os espelhos esféricos é a reflexão da luz. Bons estudos!
Referências
Física para o ensino médio, vol. 2: termologia, óptica e ondulatória – Kazuhito Yamamoto;
As faces da física – Wilson Carron.

Por Guilherme Santana da Silva
Graduado no curso de Física pela Universidade Estadual de Maringá. Professor assistente em um colégio de ensino médio e preparatório para os vestibulares. Nas horas vagas se dedica à vida religiosa, praticar mountain bike, tocar bateria, dar atenção à família e cuidar de suas duas gatinhas Penélope e Mel.
Santana, Guilherme. Espelhos esféricos. Todo Estudo. Disponível em: https://www.todoestudo.com.br/fisica/espelhos-esfericos. Acesso em: 20 de February de 2026.
1.
Um espelho esférico conjuga uma imagem virtual, direita e menor de um objeto real. Em relação a esse espelho e à posição do objeto da imagem, assinale a alternativa correta:
a) Trata-se de um espelho côncavo, quando o objeto é posicionado entre seu foco e vértice.
b) Trata-se de um espelho côncavo, quando o objeto é posicionado no foco do espelho.
c) Trata-se de um espelho côncavo, quando o objeto é colocado no centro de curvatura do espelho.
d) Trata-se de um espelho convexo, quando o objeto é colocado a qualquer distância de seu vértice.
e) Trata-se de um espelho convexo que conjuga imagens reais.
O único espelho capaz de produzir imagens virtuais, direitas e menor que o objeto é o espelho convexo, independentemente de qual seja a distância entre o objeto e o espelho.
RESPOSTA: d)
2.
Um espelho esférico côncavo conjuga uma imagem real de um objeto que é colocado a 20 cm de seu vértice. Sabendo que a distância focal desse espelho é de 10 cm, determine a distância dessa imagem formada até o objeto.
a) 10 cm
b) 30 cm
c) 40 cm
d) 20 cm
e) 0 cm
Para resolvermos esse exercício iremos utilizar a equação de Gauss:
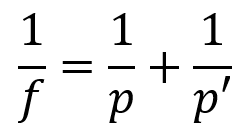
Segundo as informações do exercício, temos que p = 20cm e f = 10cm. Substituindo esses valores na equação de Gauss, obtemos
1/10 = 1/20 + 1/p’
Isolando p’
1/p’ = 1/10 – 1/20
O mínimo múltiplo comum entre 10 e 20 é 20, assim
1/p’ = (2-1)/20
Isolando p’ novamente
p’ = 20/(2-1)
p’ = 20cm
Portanto, a distância entre o objeto e a imagem é zero.
RESPOSTA: e)