Equação de Bernoulli descreve o comportamento de um fluido dentro de um tubo ou conduto. Essa relação matemática faz parte da mecânica dos fluidos. Além disso, seu nome é em homenagem a Daniel Bernoulli. Isto é, a equação é atribuída a esse cientista. Para saber mais sobre o assunto, continue a leitura.
Publicidade
O que é a equação de Bernoulli
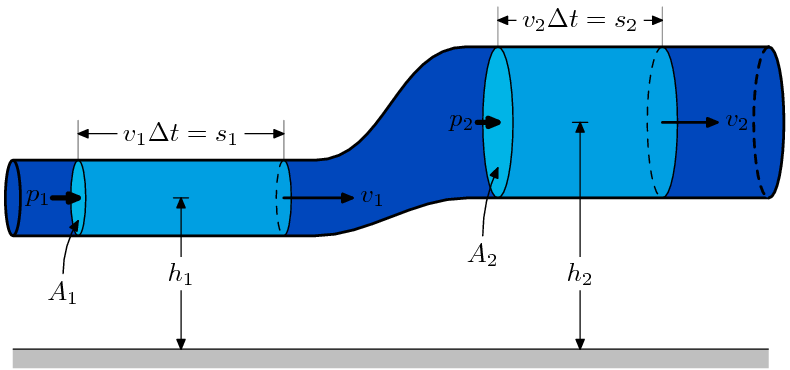
Equação de Bernoulli é uma das principais da hidrodinâmica. Além disso, essa equação obedece ao princípio de Bernoulli. O qual afirma que um fluido sem viscosidade aumenta sua velocidade quando há uma diminuição da pressão ou na energia potencial do fluido. Dessa forma, quando há uma redução na pressão, há um aumento na velocidade. Tal variação da pressão pode, por exemplo, acontecer com a variação no diâmetro de um cano, por exemplo.
Relacionadas
Fórmula
Basicamente, existem duas equações de Bernoulli. A forma original dela é voltada para os fluidos incompressíveis. Dessa maneira, ela depende da velocidade do fluido, aceleração gravitacional, sua altura em relação a um referencial, pressão no recipiente e massa específica. Matematicamente:
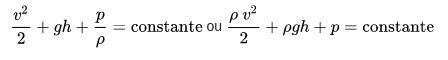
Em que,
- v: velocidade do fluido ao longo do conduto (m/s)
- g: aceleração da gravidade (m/s2)
- h: altura em relação a um referencial (m)
- p: pressão do fluido (Pa)
- ρ: massa específica (kg/m3)
O resultado da equação deve ser igual a uma constante. Isto é, caso haja uma variação em alguma das variáveis, outra também deve mudar para que a igualdade seja mantida. Além disso, a unidade de medida da pressão no líquido também pode ser apresentada como N/m2 ou kg·s2/m.
Publicidade
Vídeos sobre Equação de Bernoulli
Selecionamos videoaulas e experimentos sobre esse tema da hidrostática. Confira os vídeos para aprofundar ainda mais seu conhecimento. Acompanhe:
Vazão, continuidade e Bernoulli
Como tema introdutório da hidrodinâmica, o professor Marcelo Boaro explica o que é a vazão. A partir disso, ele também fala das equações de continuidade e de Bernoulli. Ao fim do vídeo, Boaro resolve um exercício de aplicação.
Publicidade
Escoamento em um vórtice
O escoamento de líquidos é explicado pelo princípio de Bernoulli. Além disso, os vórtices formados por esse escoamento são explicados pela força de coriolis. Nesse vídeo, o professor Claudio Furukawa mostra um experimento de escoamento de fluido por meio de um vórtice.
Tubo de Venturi caseiro
O professor Rafael Campos constrói um tubo de Venturi com materiais de baixo custo. Dessa forma, é possível demonstrar os princípios da hidrodinâmica. Dentre eles, a equação de Bernoulli.
Esse conteúdo está diretamente ligado à dinâmica dos fluidos. Aproveite seus estudos de física e conheça os fenômenos da Hidrostática.
Referências
YOUNG, H. D. et al. Física I: Mecânica. São Paulo: Addison & Wesley. 2016
NUSSENZVEIG, H. M. Curso de Física Básica: Volume 1. Rio de Janeiro: Blucher. 2014

Por Hugo Shigueo Tanaka
Divulgador Científico e co-fundador do canal do YouTube Ciência em Si. Historiador da Ciência. Professor de Física e Matemática. Licenciado em Física pela Universidade Estadual de Maringá (UEM). Mestre em Ensino de Ciências e Matemática (PCM-UEM). Doutorando em Ensino de Ciências e Matemática (PCM-UEM).
Tanaka, Hugo Shigueo. Equação de Bernoulli. Todo Estudo. Disponível em: https://www.todoestudo.com.br/fisica/equacao-de-bernoulli. Acesso em: 21 de February de 2026.
1. [ITA]
Durante uma tempestade, Maria fecha a janela de seu apartamento e ouve zumbido do vento lá fora.
Subitamente o vidro de uma janela se quebra. Considerando que o vento tenha soprado tangencialmente à janela, o acidente pode ser melhor explicado pelo(a):
a) princípio da conservação da massa
b) equação de Bernoulli
c) princípio de Arquimedes
d) princípio de Pascal
e) princípio de Stevin
Alternativa correta: B
Devido às diferenças de velocidade em ambos os lados do vidro causa uma diferença de pressão. Dessa forma, o material não resiste e se quebra.
2. [UFMS]
Água escoa em uma tubulação, onde a região 2 situa-se a uma altura h acima da região 1, conforme figura a seguir. É correto afirmar que:
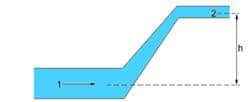
a) a pressão cinética é maior na região 1.
b) a vazão é a mesma nas duas regiões.
c) a pressão estática é maior na região 2.
d) a velocidade de escoamento é maior na região 1.
e) a pressão em 1 é menor do que a pressão em 2.
Alternativa correta: B
A vazão será a mesma porque há um regime estacionário.