Como obter uma solução para a raiz quadrada de um número negativo? Os números complexos surgiram justamente a partir dessa questão. Estudaremos então o que são esses números, sua história, a forma algébrica, as operações matemáticas, o conjugado de um número complexo e o seu módulo.
Publicidade
O que são números complexos
Os números complexos são um “novo” conjunto de números para se representar raízes de números reais negativos. Eles são conhecidos também como números imaginários.
Além disso, os números complexos devem ser tais que possam ser somados e subtraídos. Dessa forma, todo número real está contido no conjunto dos números imaginários. As operações de multiplicação e divisão também são possíveis, mas serão estudadas mais a frente.
Relacionadas
História dos números complexos
Foi apenas no século XVIII que Leonhard Euler (1707-1783) introduziu o símbolo i para denominar a raiz quadrada de -1. Isso se deu ao fato de que muitos matemáticos anteriores àquela época encontravam raízes quadradas de números negativos e resolviam equações algébricas com eles, mesmo não sabendo o significado.
A representação dos números complexos foi realizada apenas em 1806 por matemático suíço Jean-Robert Argand(1768-1822). Mas foi no final do século XVIII que o astrônomo e físico alemão Carl Friedrich Gauss fez com que a representação do plano complexo ficasse conhecida. Assim, foi possível que esse números pudessem ser amplamente estudados e favorecendo sua aplicabilidade em outras áreas de conhecimento.
Forma algébrica dos números complexos
Existe uma representação algébrica onde o número complexo é separado em uma parte de número real e a outra em um número imaginário. De uma forma matemática, podemos escreve-lá da seguinte forma:
![]()
Publicidade
Nesse caso, podemos representar cada termo como sendo:
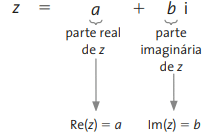
Além disso, i é a unidade imaginária, tal que i²=-1. Alguns livros também utilizam a notação i=√(-1). A existência de i implica na possibilidade da existência de uma raiz quadrada de um número negativo que não é definida no conjunto dos números reais. Alguns exemplos da aplicação dessa forma algébrica pode ser observada a seguir.
Publicidade
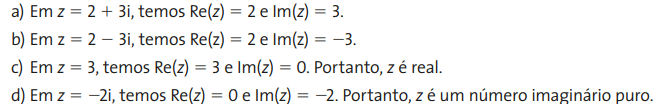
Operações com números complexos
As operações que envolvem os números complexos são as mesmas que a dos números reais (operações básicas). Porém, a divisão será tratada no tópico seguinte por envolver o conjugado de um número complexo. Aqui veremos apenas a adição, subtração e multiplicação. Uma observação a ser feita é que essas operações são intuitivas e não existe a necessidade de se decorar fórmulas!
Adição de números complexos
A adição é feita da mesma forma que seria feita para números reais. A única ressalva a ser feita é de que devemos somar apenas a parte real com outra parte real e somar apenas a parte imaginária com outra parte imaginária da forma algébrica de um número complexo. Vejamos um exemplo de uma soma.
![]()
Subtração de números complexos
Podemos dizer que a subtração segue o mesmo padrão da adição, ou seja, a subtração é feita apenas entre as partes iguais da forma algébrica (real e imaginária). Para que fique mais didático, apresentaremos alguns exemplos de uma subtração entre números complexos.
![]()
Multiplicação de números complexos
Na multiplicação, basta aplicarmos a mesma propriedade distributiva que é utilizada para os números reais para binômios. Por outro lado, é importante lembrar que i² é um número real e vale -1. Alguns exemplos a seguir mostram como a multiplicação é simples!
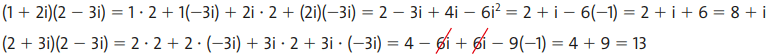
Números complexos conjugados
Assim como no conjunto dos números reais, existe a propriedade do inverso multiplicativo para os números complexos. O inverso multiplicativo de um número equivale a dizer que ao multiplicarmos esse número pelo seu inverso multiplicativo, o valor obtido é 1. Para os números complexos isso equivale a dizer, matematicamente, da seguinte forma:
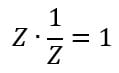
Para se representar esse inverso multiplicativo no conjunto dos números complexos é utilizado o conjugado, que nada mais é do que apenas trocar o sinal entre a parte real e a parte imaginária. Se o número complexo possuir um sinal de +, seu conjugado terá um sinal negativo. Dessa forma, podemos definir esse conjugado como sendo:
![]()
Divisão de números complexos
Agora que introduzimos a ideia de conjugado, podemos entender como efetuar a divisão de números complexos. O quociente entre dois números complexos é dado definido como:
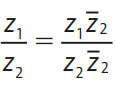
É importante lembrar, assim como na operação de divisão dos números reais, que o número complexo Z2 é diferente de zero. Podemos ver a seguir um exemplo de como se resolve um quociente desses números.
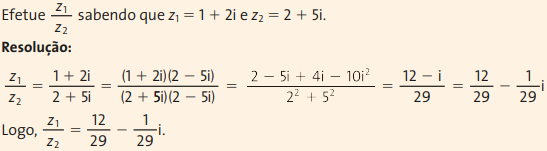
Argumento e módulo de números complexos
O argumento e o módulo de um número complexo são obtidos a partir do plano de Argand-Gauss. Esse plano é idêntico ao plano cartesiano dos números reais.
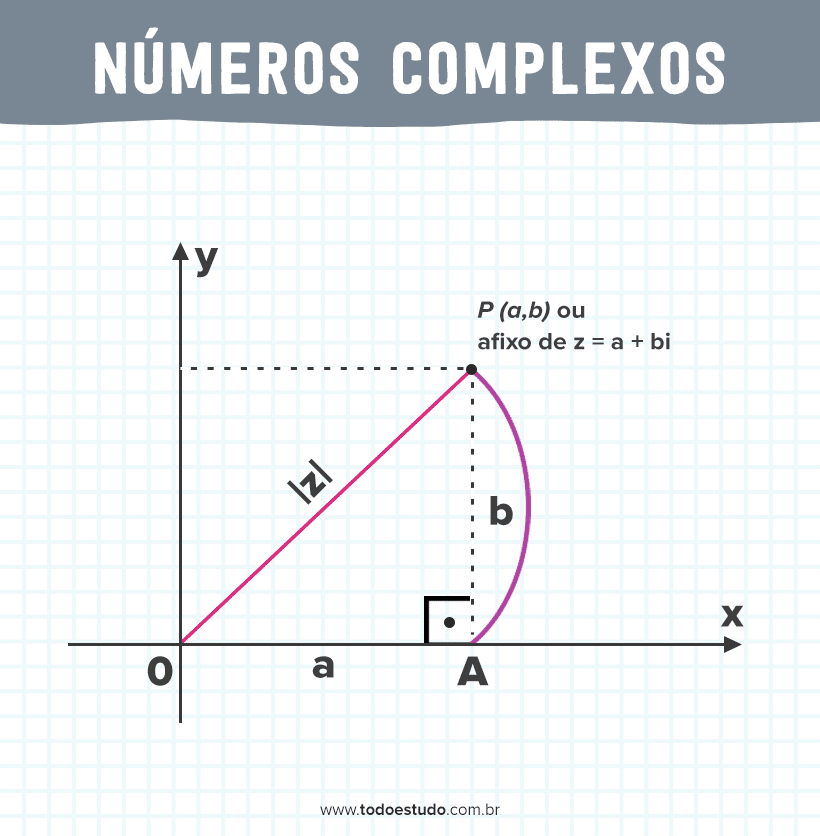
Na imagem acima, o módulo do número complexo Z é obtido pelo teorema de Pitágoras no triângulo OAP. Dessa forma, temos o seguinte:
![]()
Por outro lado, o arco entre o eixo horizontal positivo e o segmento OP é argumento. Ele é obtido quando quando criamos um arco entre esses dois pontos, representado pela cor roxa, no sentido anti-horário.
Vídeos sobre números complexos
Para que você possa compreender ainda mais sobre os números complexos, apresentaremos a seguir alguns vídeos sobre eles. Dessa forma, você poderá sanar todas as suas dúvidas!
Teoria sobre os números complexos
Entenda aqui neste vídeo um pouco mais sobre esses números e como representa-los algebricamente!
Operações com números complexos
Neste vídeo é apresentado sobre as operações com os números complexos. Aqui é abordado sobre a adição, subtração, multiplicação e divisão!
Exercícios resolvidos
Para que você possa tirar uma boa nota nas provas, esse vídeo apresenta como se resolver exercícios envolvendo números complexos!
Por fim, é importante que você revise sobre plano cartesiano, dessa forma, seus estudos vão se complementar e você compreenderá ainda mais sobre os números complexos!
Referências
IEZZI et al. Matemática: ciência e aplicações. Ensino Médio.
DANTE, Luiz Roberto. Matemática: contexto & aplicações. Ensino Médio.

Por Guilherme Santana da Silva
Graduado no curso de Física pela Universidade Estadual de Maringá. Professor assistente em um colégio de ensino médio e preparatório para os vestibulares. Nas horas vagas se dedica à vida religiosa, praticar mountain bike, tocar bateria, dar atenção à família e cuidar de suas duas gatinhas Penélope e Mel.
Santana, Guilherme. Números complexos. Todo Estudo. Disponível em: https://www.todoestudo.com.br/matematica/numeros-complexos. Acesso em: 04 de February de 2026.
1. [Unesp-SP]
Se z = (2 + i) ∙ (1 + i) ∙ i, então z, o conjugado de z, será dado por:
a) −3 − i
b) 1 − 3i
c) 3 − i
d) −3 + i
e) 3 + i
Primeiramente vamos fazer as multiplicações necessárias em z:
z = (2 + i) ∙ (1 + i) ∙ i
z = (2 + 2i + i + i²) ∙ i
z = (2 + 3i – 1) ∙ i
z = (1 + 3i) ∙ i
z = i + 3i²
z = i + 3 ∙ (– 1)
z = – 3 + i
Agora que encontramos a forma mais simples de z, basta alterar o sinal da parte imaginária para termos seu conjugado:
z = – 3 – i
RESPOSTA: a)
2. [UFSCar-SP (Modificada)]
Sejam x, y R e z = x + yi um número complexo.
a) Calcule o produto (x + yi) ∙ (1 + i).
a) Realizando a multiplicação pedida, temos:
(x + yi) ∙ (1 + i)
x + yi + xi + yi²
x + yi + xi + y(– 1)
(x – y) + (x + y)∙i
O produto (x + yi) ∙ (1 + i) equivale a (x – y) + (x + y)∙i.