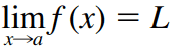Um dos primeiros assuntos a ser estudado em cálculo é a questão dos limites. Os limites possuem diversas aplicações, mas a sua essência se baseia em analisar funções e é o conceito básico para as derivadas. Dessa forma, entenda aqui o que é limite, sua definição, como se calcula e veja exercícios resolvidos para fixar o conteúdo.
Publicidade
O que é limite?
Para entendermos o que é limite, tomemos como exemplo a função f(x) = x² – x + 2. Faremos agora uma análise desta função realizando uma aproximação de x = 2 pela esquerda e pela direita. A tabela a seguir mostra o que acontece quando realizamos tal operação.
Relacionadas
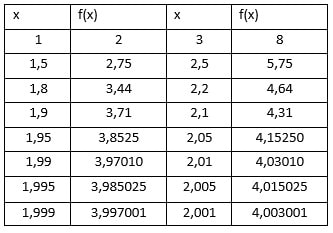
Os valores à esquerda representam a aproximação feita pela esquerda de x. Por sua vez, os valores à direita da tabela representam a aproximação pela direita de x. Para melhor entendermos isso, a seguir apresentamos um gráfico ilustrativo.
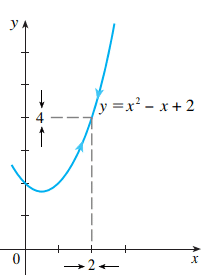
Dessa forma, podemos ter uma definição um pouco mais formal do que é limite de uma função que será apresentada a seguir.
Publicidade
Escrevemos
e dizemos “o limite de f(x), quando x tende ao a, é igual a L”, se pudermos tornar os valores de f (x) arbitrariamente próximos de L (tão próximos de L quanto quisermos), tomando x suficientemente próximo de a (por ambos os lados de a), mas não igual ao a.
Existem alguns tipos de limites que são de extrema importância para os estudos pertinentes ao assunto. Assim, a seguir iremos estudar alguns destes limites.
Tipos de limites
Podemos encontrar vários tipos de limites na literatura. Entretanto, aqui veremos apenas três tipos: limites laterais, limites indeterminados e limites infinitos. Dessa forma, vamos estudá-los um pouco mais.
Publicidade
Limites laterais
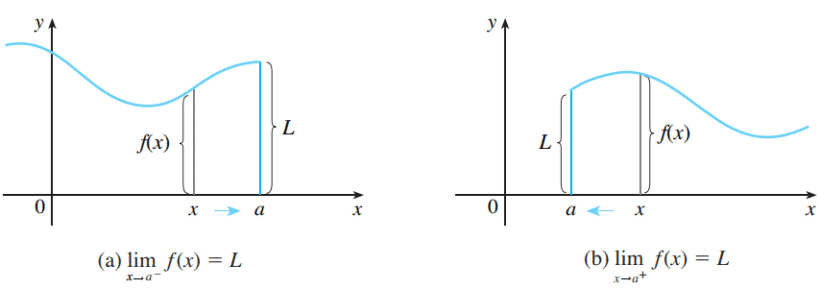
Este tipo de limite equivale a dizer que consideramos apenas os valores à esquerda ou à direita de x. Se for um limite à esquerda, serão valores menores do que x e vice-versa. Podemos escrever isso da seguinte maneira:
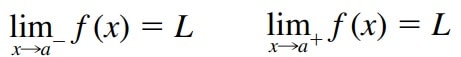
A primeira forma se refere ao limite tomado pela esquerda, ou seja, quando x é menor do que a. A segunda forma se refere para limites à direita. Em outras palavras, quando x tende ao a e x é maior do que a. Uma forma mais pode ser vista a seguir.
Escrevemos
e dizemos que o limite à esquerda de f(x) quando x tende ao a [ou o limite de f(x) quando x tende ao a pela esquerda] é igual ao L se pudermos tornar os valores de f(x) arbitrariamente próximos de L, para x suficientemente próximo de a e x menor que a.
A definição de limite à direita é análoga à definição de limite à esquerda.
Limites indeterminados
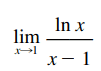
O limite acima é um exemplo do que chamamos de limite indeterminado da forma 0/0 (“zero por zero”). O problema com esses limites deve-se a dificuldade de dizer por inspeção se o limite existe e, se existir, é difícil de dizer o seu valor.
De uma forma geral, se tivermos o limite da figura a seguir em que f(x) e g(x) tendem a zero quando x tende para a. Então, o limite é indeterminado do tipo 0/0.
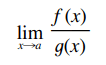
Limites infinitos
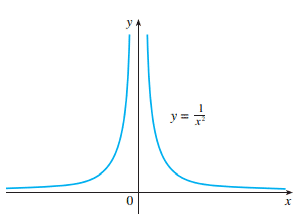
Vamos usar a função f(x) = 1/x² como exemplo, conforme o gráfico anterior. Para valores de x suficientemente perto de zero obteremos valores grandes para f(x). Faça você mesmo em casa e verifique para x = ±1, x = ±0,5, x = ±0,2, x = ±0,05, x = ±0,01 e x = ±0,001. Assim, os valores de f(x) não tendem a um número. Portanto, não existe limite para f(x) = 1/x².
Simbolicamente falando, em geral, usamos a expressão a seguir para um limite infinito.
![]()
Em outras palavras, podemos dizer que os valores de f(x) tendem a serem cada vez maiores à medida que x se torna cada vez mais próximo de a. Podemos mostrar os limites infinitos de uma maneira mais formal a seguir.
Seja f uma função definida em ambos os lados de a, exceto possivelmente em a. Então,
significa que podemos fazer os valores de f (x) ficarem arbitrariamente grandes (tão grandes quanto quisermos) tomando x suficientemente próximo de a, mas não igual ao a.
Lembrando que seria necessário um estudo mais aprofundado sobre limites, pois ainda existem muitas outras coisas sobre esse conteúdo.
Saiba mais sobre limites
Para que você possa fixar melhor sobre o assunto estudado até aqui, serão apresentadas algumas videoaulas a seguir. Dessa forma, você conseguirá se aprofundar seus conhecimentos sobre limites.
Ideia intuitiva de limites
Neste vídeo, será apresentada a noção básica de limites. Dessa forma, você conseguirá ter uma melhor compreensão da teoria de limites.
Limites indeterminados
Entenda aqui neste vídeo sobre um limite indeterminado e como sair desta indeterminação!
Exercícios sobre indeterminação de limites
Para ficar ainda mais completo sobre limites indeterminados, este vídeo apresenta a resolução de alguns exercícios!
Por fim, para que seus estudos fiquem ainda mais completos, é importante que você revise o que são funções e quais são seus tipos. Alguma delas você pode encontrar aqui no site, como a função composta, função linear, função afim e entre outras!
Referências
STEWART, James. Cálculo – volume I. São Paulo: Cengage Learning, 2013.

Por Guilherme Santana da Silva
Graduado no curso de Física pela Universidade Estadual de Maringá. Professor assistente em um colégio de ensino médio e preparatório para os vestibulares. Nas horas vagas se dedica à vida religiosa, praticar mountain bike, tocar bateria, dar atenção à família e cuidar de suas duas gatinhas Penélope e Mel.
Santana, Guilherme. Limites. Todo Estudo. Disponível em: https://www.todoestudo.com.br/matematica/limites. Acesso em: 13 de March de 2026.
1.
Calcule o seguinte limite

Ao aplicarmos o limite, chegamos em uma forma indeterminada
![]()
Para retirar a indeterminação, fatoramos o polinômio do numerador em produto de sua raiz. Dessa forma
![]()
Assim, conseguimos cancelar o (x-3) do numerador com o do denominador. Portanto
![]()
2.
Calcule o seguinte limite
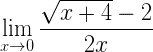
Se calcularmos esse limite por substituição direta, chegaremos em uma indeterminação
![]()
Para cancelarmos essa indeterminação, multiplicamos a expressão pelo seu conjugado. Dessa forma
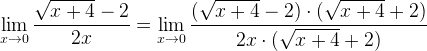
Portanto, o resultado final será
![]()