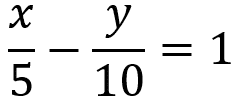Podemos escrever a equação de uma reta de 3 formas diferentes, mas como entender elas e como diferenciá-las? Apresentaremos aqui como responder a essas perguntas mostrando quais são os tipos de equação de reta e, no fim, apresentaremos alguns exercícios resolvidos para que você fixe e entenda melhor sobre o conteúdo!
Publicidade
Equações da reta
Existem 3 formas matemáticas de se escrever a equação de uma reta. São elas: equação geral, reduzida e segmentária. Dessa forma, veremos cada uma delas em detalhes.
Relacionadas
Equação geral da reta
![]()
A imagem acima representa a equação geral da reta. Ela é obtida a partir do alinhamento de dois pontos no plano cartesiano e a solução do determinante entre eles. Os elementos a, b e c são constantes e são definidos da seguinte forma:
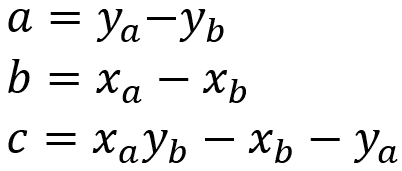
Como no plano cartesiano um ponto é definido por (x, y), então temos que (xa, ya) é o primeiro ponto e (xb, yb) o segundo ponto. As constantes a e b não devem ser nulas ao mesmo tempo.
Publicidade
Equação reduzida da reta
![]()
A imagem acima representa a equação reduzida da reta. Ela é importante, pois é possível calcular o coeficiente angular de uma reta a partir de uma equação. Além disso, a coordenada y pode ser expressa em função da coordenada x.
Na equação reduzida, temos que m é o coeficiente angular da reta, ou seja, é ele que define o angulo de inclinação da reta em relação ao eixo x. A constante n é o coeficiente linear da reta. Em outras palavras, é onde a reta toca no eixo y do sistema de coordenadas.
Publicidade
Equação da reta segmentária
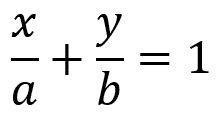
Esta equação é conhecida como equação segmentária. Ela é uma equação que não passa pela origem do sistema cartesiano de coordenadas e intersecta os pontos (a,0) e (0,b).
Estes sãos os tipos de equações de reta que são mais cobrados nos vestibulares pelo Brasil. Para que nenhuma dúvida fique sem solução, apresentaremos a seguir algumas videoaulas sobre o assunto!
Saiba mais sobre equações da reta
Todas as dúvidas devem ser sanadas. Por isso, apresentaremos a seguir videoaulas sobre equações da reta para que você possa se dar muito bem em todas as provas!
Equação geral da reta
Neste vídeo é apresentado uma visão geral sobre esse tipo de equação da reta, além de um breve macete de como se calcular a equação geral de uma reta a partir de dois pontos!
Equação reduzida da reta
Além da equação geral, também é importante estudarmos um pouco mais sobre a equação reduzida da reta. Aqui, neste vídeo, você irá aprender um pouco mais sobre este assunto!
exercícios resolvidos
Para que você possa entender na prática o que foi estudado até aqui, apresentaremos neste vídeo um exercício resolvido sobre equação da reta!
Por fim, é importante que você revise também sobre plano cartesiano e geometria analítica, conteúdos relacionados para seguir se aprofundando no assunto!
Referências
IEZZI et al. Matemática: ciência e aplicações. Ensino Médio.
DANTE, Luiz Roberto. Matemática: contexto & aplicações. Ensino médio.

Por Guilherme Santana da Silva
Graduado no curso de Física pela Universidade Estadual de Maringá. Professor assistente em um colégio de ensino médio e preparatório para os vestibulares. Nas horas vagas se dedica à vida religiosa, praticar mountain bike, tocar bateria, dar atenção à família e cuidar de suas duas gatinhas Penélope e Mel.
Santana, Guilherme. Equação da reta. Todo Estudo. Disponível em: https://www.todoestudo.com.br/matematica/equacao-da-reta. Acesso em: 02 de February de 2026.
1.
Sabendo que a equação da reta r é dada por y = x + 5, identifique seu coeficiente angular, sua inclinação e o ponto em que a reta intercepta o eixo y.
Como temos a equação reduzida da reta, então:
m = 1
Sendo m = tg θ ⇒ tg θ = 1 ⇒ θ = 45º
O ponto de interseção da reta com o eixo y é o ponto P(0,n), sendo n=5, então o ponto será P(0,5)
2.
Escreva na forma segmentária, a equação da reta que passa pelo ponto A(5,0) e tem coeficiente angular 2.
Como sabemos, o coeficiente angular pode ser escrito como:
m = -b/a
Sabemos também que m = 2 e a = 5, assim
2 = -b/5
b = -10
Podemos então substituir esses valores na equação segmentária da reta. Assim