À primeira vista, Zenão de Eléia, filósofo grego que viveu por volta de 450 a.C., já tinha um pensamento a respeito do que seria o conceito de infinito quando ele propôs o famoso paradoxo de Zenão.
Publicidade
Por outro lado, em 1830, o matemático Georg Cantor (1845-1918), juntamente com seu colega Richard Dedekind (1831-1916), conseguiram definir e classificar precisamente muitos tipos diferentes de infinitos.
Em suma, para realizar tal feito, eles utilizaram uma nova teoria, criada por Cantor em 1872, conhecida como teoria dos conjuntos.
Relacionadas
Sob o mesmo ponto de vista, o matemático John Venn (1834-1923) criou um diagrama, conhecido como Diagrama de Venn.
Esse diagrama é utilizado para a representação de um conjunto em que os elementos são simbolizados por pontos (números, letras, nomes, etc.) interiores a uma região plana (normalmente uma circunferência ou uma elipse), delimitada por uma linha fechada que não se entrelaça.
Um exemplo prático
Além da utilização desse diagrama para a teoria de conjuntos, ao mesmo tempo podemos utilizá-lo para a aplicação nos conceitos de probabilidade e em lógica.
Suponha uma sala de aula com 25 alunos. Ainda temos que 15 alunos gostam do refrigerante A e 18 gostam do refrigerante B. Se somarmos 15 e 18, encontraremos 33 pessoas nesse grupo. Isso ocorre pois temos, ao mesmo tempo, alunos nessa sala que optam pelos dois.
Publicidade
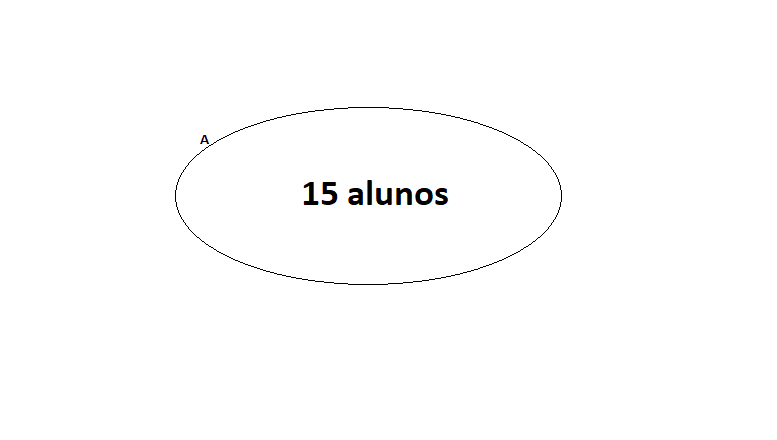
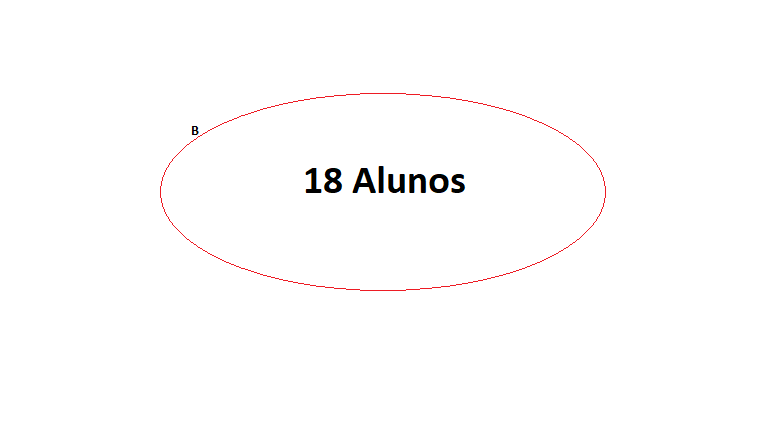
Para encontrar quantos alunos gostam de ambos os refrigerantes, basta fazer a diferença entre 33 e o total de alunos da sala. Caso uma professora escolhesse aleatoriamente um aluno dessa turma, qual será a probabilidade de escolher um aluno que goste dos dois?
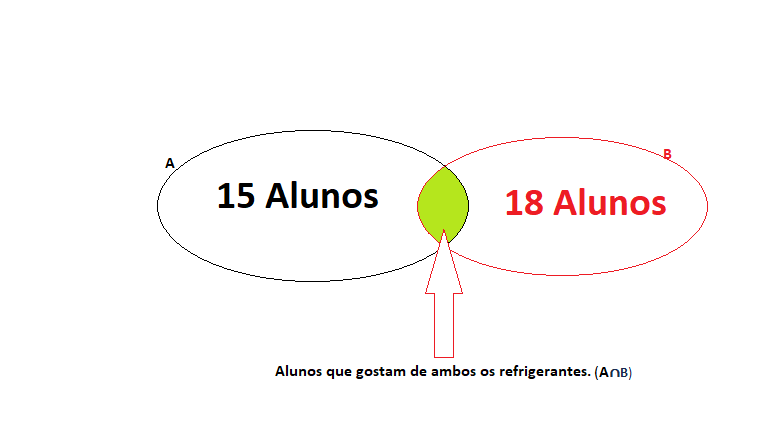
Neste exemplo, podemos utilizar o diagrama de Venn para representar tal situação para o conjunto A e o conjunto B.
A probabilidade de escolher um aluno que goste dos dois refrigerantes, utilizando o diagrama de Venn, é a intersecção dos dois conjuntos, ou seja, A∩B.
Publicidade
Modelos de Diagrama de Venn
Antecipadamente nos foi mostrado o exemplo da probabilidade de em uma sala de aula obtermos em um sorteio, alunos que gostem do refrigerante A e B ao mesmo tempo.
Mas como seria a relação entre esses conjuntos se fossem adicionados mais outros conjuntos ao exemplo citado?
Podemos então, de antemão, utilizar alguns modelos para o diagrama de Venn, para 2, 3 e 4 conjuntos.
A princípio vamos começar com a relação entre 2 conjuntos, mostrando a representação matemática dessa relação.
Relação entre 2 conjuntos
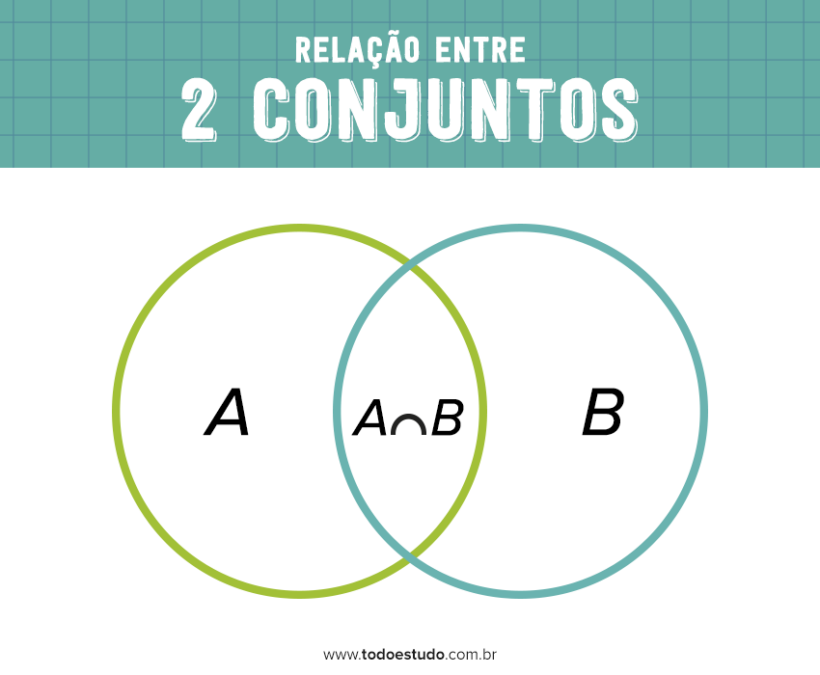
n(A U B) = n(A) + n(B) – n(A ∩ B)
De acordo com a relação entre 2 conjuntos, temos o número de elementos do conjunto A e B e de sua intersecção A ∩ B.
Relação entre 3 conjuntos
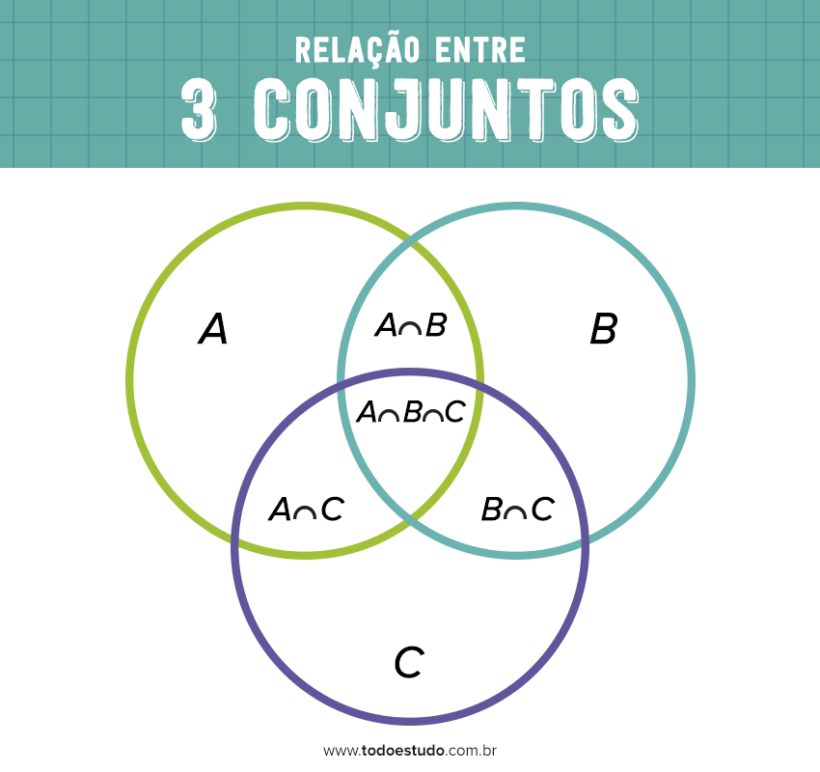
n(A U B U C) = n(A) + n(B) + n(C) – n(A∩B) – n(A∩C) – n(B∩C) + n(A∩B∩C)
Nesse ínterim, teremos a quantidade de elementos das intersecções A∩C, B∩C e A∩B∩C, juntamente com as relações para 2 conjuntos.
Sob o mesmo ponto de vista, podemos citar um exemplo de aplicação dessa relação de conjuntos na geografia.
Durante o decorrer das décadas de 1960, 1970 e 1980, houve a necessidade de se estudar o mundo em suas três divisões regionais.
Ainda mais, o mundo ficou dividido em Primeiro Mundo, Segundo Mundo e Terceiro Mundo. Dessa forma, podemos representar essa divisão em um diagrama de Venn, que foi proposta pelo geógrafo Yves Lacoste.
Relação entre 4 conjuntos
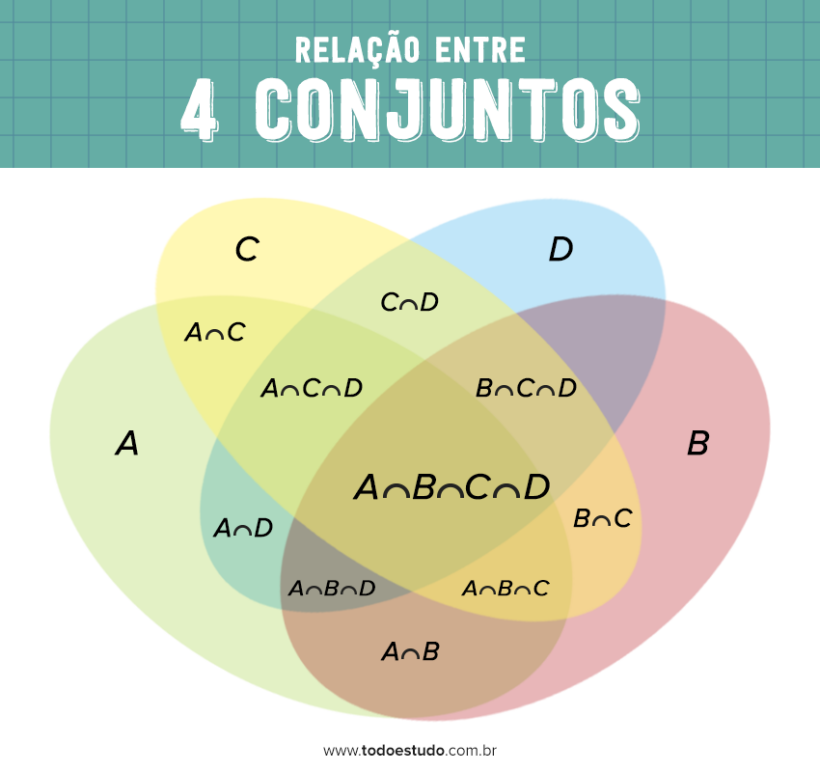
n(A U B U C U D) = n(A) + n(B) + n(C) + n(D) – n(A∩B) – n(A∩C) – n(A∩D) – n(B∩C) – n(B∩D) – n(C∩D) + n(A∩B∩C) + n(A∩B∩D) + n(A∩C∩D) + n(B∩C∩D) – n(A∩B∩C∩D)
Por outro lado, no caso de uma relação de 4 conjuntos, teremos o número de elementos das intersecções A∩D, B∩D, C∩D, A∩B∩D, A∩C∩D, B∩C∩D e A∩B∩C∩D , além das relações já existentes para 2 e 3 conjuntos.
Do mesmo modo que nos casos anteriores, vamos observar o exemplo da Figura abaixo.
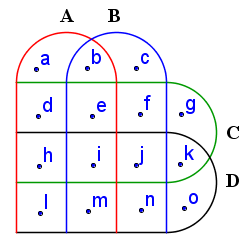
A partir da imagem, podemos observar as seguintes situações:
- A = {a, b, d, e, h, i, l, m}
- B = {b, c , e, f, i, j, m, n}
- C = {d, e, f, g, h, i, j, k}
- D = {h, i, j, k, l, m, n, o}
- A∩B = {b, e, i, m}
- A∩C = {d, e, h, i}
- B∩C = {e, f, i, j}
- C∩D = {h, i, j, k}
- A∩D = {h, i, l, m}
- B∩D = {i, j, m, n}
- A∩B∩C = {e, i}
- A∩C∩D = {h, i}
- B∩C∩D = {i, j}
- A∩B∩C∩D = {i}
Em suma, todas as situações de combinações de conjuntos nos ajudam a resolver muitos problemas matemáticos que se mostram complicados.
Resumo
Em síntese, podemos ver um resumo a respeito do diagrama de Venn no vídeo a seguir.
Referências
Dante, Luiz Roberto. Matemática : contexto & aplicações : ensino
médio / Luiz Roberto Dante. — 3. ed. –. São Paulo : Ática, 2016.
PAIVA, Manoel. Matemática. São Paulo: Moderna, 2005.

Por Guilherme Santana da Silva
Graduado no curso de Física pela Universidade Estadual de Maringá. Professor assistente em um colégio de ensino médio e preparatório para os vestibulares. Nas horas vagas se dedica à vida religiosa, praticar mountain bike, tocar bateria, dar atenção à família e cuidar de suas duas gatinhas Penélope e Mel.
Santana, Guilherme. Diagrama de Venn. Todo Estudo. Disponível em: https://www.todoestudo.com.br/matematica/diagrama-de-venn. Acesso em: 12 de February de 2026.
1. [UEPA]
De acordo com a reportagem da Revista VEJA (edição 2341), é possível fazer gratuitamente curso de graduação pela Internet. Dentre os ofertados temos os cursos de Administração (bacharelado), Sistemas de Computação (tecnólogo) e Pedagogia (licenciatura). Uma pesquisa realizada com 1800 jovens brasileiros sobre quais dos cursos ofertados gostariam de fazer constatou que 800 optaram pelo curso de Administração; 600 optaram pelo curso de Sistemas de Computação; 500 optaram pelo curso de Pedagogia; 300 afirmaram que fariam Administração e Sistemas de Computação; 250 fariam Administração e Pedagogia; 150 fariam Sistemas de Computação e Pedagogia e 100 dos jovens entrevistados afirmaram que fariam os três cursos. Considerando os resultados dessa pesquisa, o número de jovens que não fariam nenhum dos cursos elencados é:
a) 150
b) 250
c) 350
d) 400
e) 500
Resposta:
- A intersecção dos 3 conjuntos, alunos que optaram pelos 3 cursos: 100
- Alunos que optaram por apenas 2 cursos:
a) Administração e Pedagogia: 250 – 100 = 150
b) Administração e Sistemas de Computação: 300 – 100 = 200
c) Pedagogia e Sistemas de Computação: 150 – 100 = 50 - Alunos que optaram por apenas 1 curso:
a) Pedagogia: 500 – (150 + 100 + 50) = 200
b) Administração: 800 – (150 + 100 + 200) = 350
c) Sistemas de Computação: 600 – (50 + 100 + 200) = 250 - Alunos que não optaram por nenhum dos três cursos ofertados: A soma de todos os números das sete regiões dos círculos representa a quantidade de jovens que optaram por pelo menos um curso: 200 + 50 + 250 + 150 + 100 + 200 + 350 = 1300
Dessa forma, a quantidade de jovens que foram entrevistados e não optaram por nenhum dos três cursos é obtida por: 1800 – 1300 = 500. Observe o diagrama ao lado com os valores encontrados já dispostos nas respectivas regiões dos círculos e universo
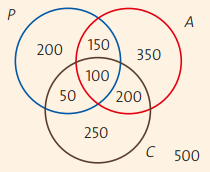
RESPOSTA: e
2. [TJ SP 2014 – Vunesp]
O diagrama mostra a distribuição de pessoas, que possuem uma ou mais das habilidades A, B, C. As letras minúsculas representam o número de pessoas que possuem determinada ou determinadas habilidades. Por exemplo: a letra w, que está na intersecção dos grupos de habilidades A e B, representa a quantidade de pessoas que possuem ambas as habilidades citadas.
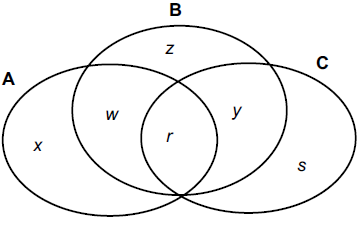
Foi realizada uma enquete com todas essas pessoas, e elas deveriam responder SIM ou NÃO a essa única pergunta: “Você possui as habilidades A e C? Todas as pessoas responderam de forma verdadeira, e o número de pessoas que respondeu SIM foi
a) x + s.
b) w + r + y.
c) x + r + s.
d) zero.
e) r.
Basta verificarmos no Diagrama de Venn em qual situação as pessoas possuem a habilidade A e C ao mesmo tempo. Neste caso, a única possibilidade é mostrado pela letra r.
RESPOSTA: e