Ao puxar um objeto por meio de uma corda, a força aplicada é transmitida através do cabo. Podemos, então, dizer que a corda está sob a ação de uma força de tração. De maneira resumida, a tração consiste em exercer em um corpo um par de forças em sentidos opostos.
Publicidade
O que é tração?
Apesar de ser uma palavra que remete a diversos significados, em física, a tração é um tipo de força aplicada sobre um corpo com o sentido voltado para a sua parte externa. Um esforço de tração causa a reorganização dos átomos, de modo que o corpo sendo tracionado se alongue no sentido da força aplicada.
Relacionadas
Apesar de muitos lugares apresentarem as grandezas de tensão e tração como sinônimos, no rigor das definições, elas não são a mesma coisa. De maneira simplificada, a tensão em um corpo é a medida da força agindo sobre a área transversal de uma corda, cabo, corrente ou similar.
A unidade de medida (em unidades do Sistema Internacional) da tensão é N/m² (Newton por metro quadrado), que é a mesma unidade de medida para a pressão. Já a tração é uma força aplicada sobre um corpo a fim de exercer sobre ele esforços em sentidos opostos, sem levar em conta a área na qual está sendo aplicada essa força.
Cálculo da tração
Infelizmente, não há uma equação específica para o cálculo da tração. Porém, devemos seguir uma estratégia parecida com a utilizada em casos onde é necessário encontrar a força normal. Ou seja, utilizamos a equação da segunda lei de Newton a fim de encontrar uma relação entre o movimento do objeto e as forças envolvidas. Para isso, podemos nos basear nos seguintes procedimentos:
- Analisar as forças envolvidas no movimento por meio do diagrama de forças;
- Utilizar a segunda lei de Newton (Fr = ma) e escrevê-la na direção da força de tração;
- Encontrar a tração a partir da segunda lei de Newton.
Veja abaixo como calcular a tração em alguns casos:
Publicidade
Tração sobre um corpo
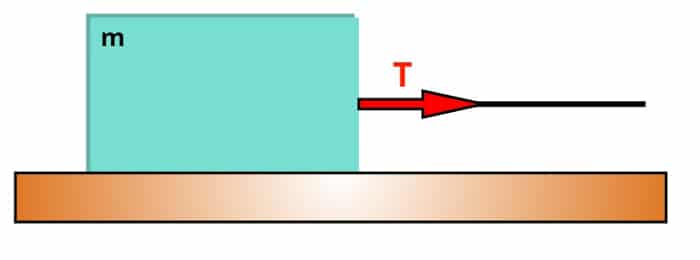
Considere um corpo qualquer de massa m, que repousa sobre uma superfície completamente lisa e sem atrito. Dessa forma, seguindo os procedimentos acima, obtemos que:
T = mᐧa
Publicidade
Em que,
- T: tração (N);
- m: massa (kg);
- a: aceleração (m/s2).
Esse corpo é puxado por uma força de tração T paralela à superfície, exercida por meio de um fio de dimensões desprezíveis e inextensível. Nesse caso, o cálculo da tração é o mais simples possível. Aqui, a única força que atua sobre o sistema é a força de tração.
Tração em um plano inclinado
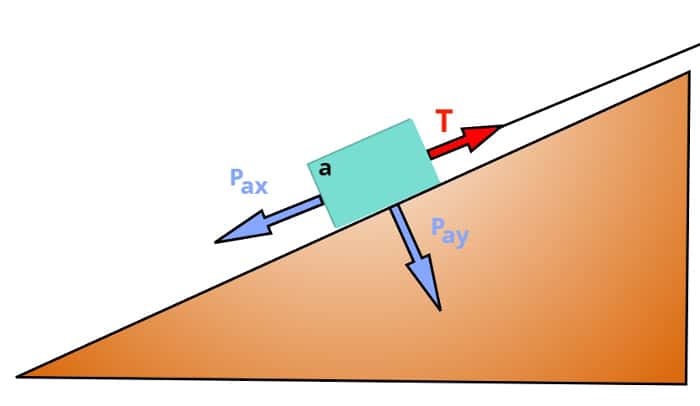
Note que PAx e PAy são, respectivamente, as componentes horizontal e vertical do peso do corpo A. Note também que, para facilitar os cálculos, consideramos a superfície do plano inclinado como o eixo horizontal do nosso sistema de coordenadas.
Suponha agora o mesmo corpo de massa m colocado sobre um plano inclinado, onde também não há atrito entre o bloco e a superfície. Assim, a força de tração será:
T – PAx= mᐧa
Em que,
- T: tração (N);
- PAx: componente horizontal da força peso (N);
- m: massa (kg);
- a: aceleração (m/s2).
Analisando a figura e seguindo os procedimentos citados anteriormente, é possível observar que podemos utilizar a segunda lei de Newton apenas na direção horizontal do nosso sistema de coordenadas. Além disso, há uma subtração entre a Tração e a componente horizontal do peso do bloco, porque as duas forças possuem sentidos contrários.
Tração com ângulo
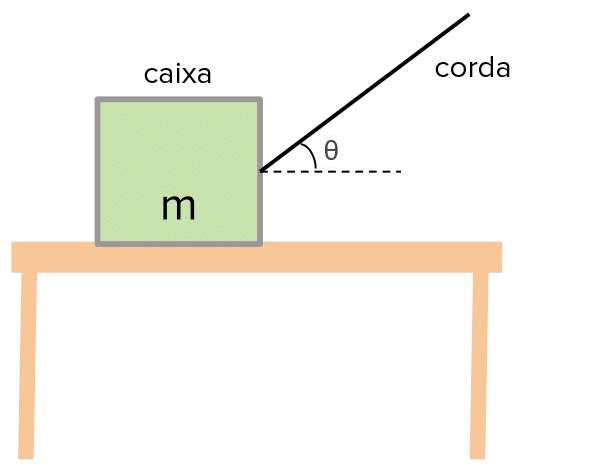
Considere um corpo com massa m sobre uma superfície sem atrito. O objeto está sendo puxado por uma força de tração T, que não é paralela à superfície. Assim, a força de tração será:
Tcosϴ = mᐧa
Em que,
- Tcosϴ: projeção horizontal da força de tração (N);
- m: massa (kg);
- a: aceleração (m/s2).
Esse corpo é puxado por uma força de tração T, exercida por meio de um fio de dimensões desprezíveis e inextensível. Esse exemplo é similar ao caso da força de tração aplicada sobre um corpo em uma superfície sem atrito. Porém, aqui, a única força que atua sobre o sistema é a componente horizontal da força de tração. Devido a isso, no cálculo da tração devemos considerar apenas a projeção horizontal da força de tração.
Tração em uma superfície com atrito
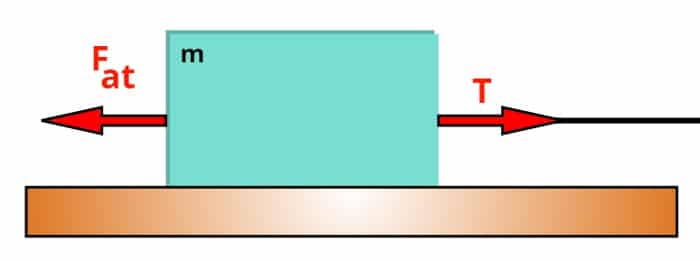
Considere um corpo qualquer de massa m, que repousa sobre uma superfície na qual há atrito. Dessa forma, seguindo os procedimentos acima, obtemos que:
T – Fat = mᐧa
Em que,
- T: tração (N);
- Fat: força de atrito (N);
- m: massa (kg);
- a: aceleração (m/s2).
Esse corpo é puxado por uma força de tração T, exercida por meio de um fio de dimensões desprezíveis e inextensível. Além disso, devemos considerar a força de atrito exercida entre o bloco e a superfície na qual ele se encontra. Dessa forma, é válido destacar que, caso o sistema esteja em equilíbrio (isto é, se, apesar de estar sendo aplicado uma força sobre o fio, o bloco não se movimenta ou desenvolve uma velocidade constante), então, T – Fat = 0. Caso o sistema esteja em movimento, então T – Fat = ma
Tração entre corpos do mesmo sistema
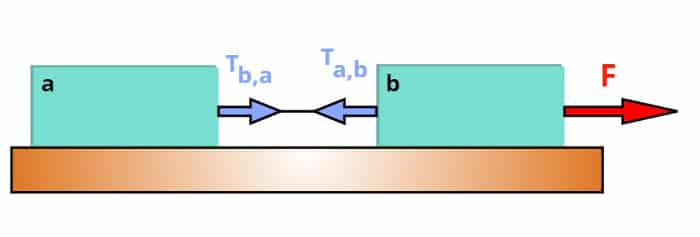
Note que a força que o corpo a faz no corpo b é denotada por Ta,b. Já a força que o corpo b faz no corpo a é denotada por Tb,a.
Suponha agora dois (ou mais) corpos ligados por cabos. Eles se moverão juntos e com a mesma aceleração. Porém, para determinar a tração que um corpo faz em outro, devemos calcular a força resultante separadamente. Dessa forma, seguindo os procedimentos acima, obtemos que:
Tb,a = maᐧa (corpo a)
Ta,b – F = mbᐧa (corpo b)
Em que,
- Ta,b: tração que o corpo a faz no corpo b (N);
- Tb,a: tração que o corpo b faz no corpo a (N);
- F: força aplicada ao sistema (N);
- ma: massa do corpo a (kg);
- mb: massa do corpo b (kg);
- a: aceleração (m/s2).
Apenas um cabo liga os dois corpos, então, pela terceira lei de Newton, a força que o corpo a faz no corpo b possui a mesma intensidade da força que o corpo b faz no corpo a. Porém, essas forças possuem sentidos opostos.
Tração no pêndulo
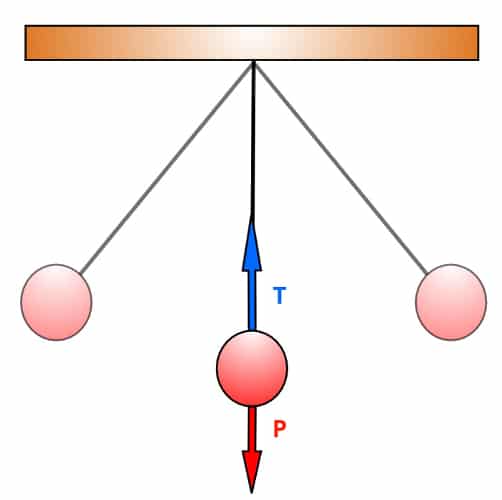
No movimento pendular, a trajetória descrita pelos corpos é circular. A força de tração exercida pelo fio atua como uma componente da força centrípeta. Dessa forma, no ponto mais baixo da trajetória, obtemos que:
T – P = Fcp
Em que,
- T: tração (N);
- P: peso (N);
- Fcp: força centrípeta (N).
No ponto mais baixo do movimento do pêndulo, a força de tração está no sentido contrário do peso do corpo. Dessa forma, a diferença entre as duas forças será igual à força centrípeta, a qual equivale ao produto da massa do corpo pelo quadrado de sua velocidade, dividido pelo raio da trajetória.
Tração no fio

Caso um corpo esteja suspenso por um fio ideal e em equilíbrio, a força de tração será nula.
T – P = 0
Em que,
- T: tração (N);
- P: peso (N).
Isso acontece porque a tração em um fio é a mesma nas duas extremidades, devido à terceira lei de Newton. Como o corpo está em equilíbrio, a soma de todas as forças que atuam sobre ele é igual a zero.
Exemplos de tração no dia a dia
Existem exemplos simples de aplicação da força de tração que podem ser observados em nosso dia a dia. Veja:
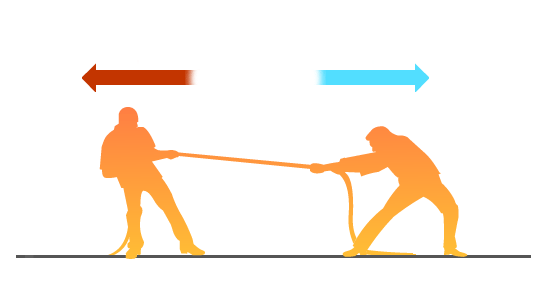
Cabo de guerra
A força de tração é exercida em ambos os lados da corda pelos jogadores. Além disso, podemos relacionar esse caso com o exemplo de tração entre corpos do mesmo sistema.
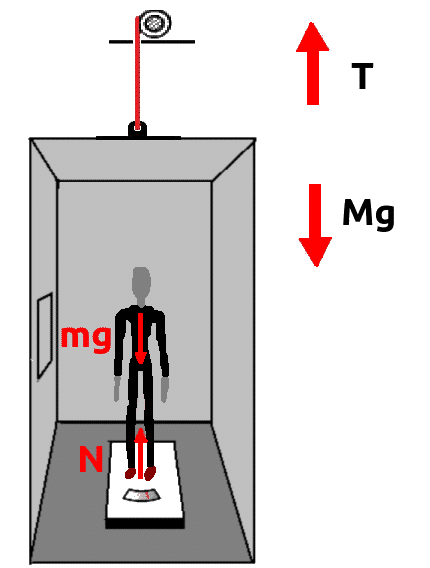
Elevador
O cabo do elevador é tracionado em uma das extremidades pelo peso do elevador e de seus ocupantes e, na outra ponta, pela força exercida pelo seu motor. Caso o elevador esteja parado, as forças em ambos os lados possuem a mesma intensidade. Além disso, aqui podemos considerar o caso como sendo similar ao exemplo da tração exercida sobre um fio.
Balanço
Brincar no balanço é muito comum para pessoas de todas as idades. Além disso, podemos considerar o movimento desse brinquedo como sendo um movimento pendular e relacioná-lo com o caso da tração em um pêndulo.
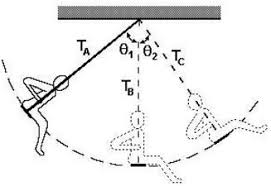
Como foi possível ver, a tração está diretamente ligada ao nosso cotidiano. Seja em brincadeiras ou até mesmo em elevadores.
Vídeos sobre Tração
Que tal reservar um tempo para se aprofundar no assunto assistindo aos vídeos sugeridos?
Pêndulo simples e pêndulo cônico
Aprofunde seus conhecimentos sobre o estudo do movimento em pêndulos!
Experimento sobre força de tração
Veja uma aplicação prática da força de tração.
Exercício resolvido sobre tração em corpos do mesmo sistema
Uma aplicação analítica do conceito de tração em corpos do mesmo sistema.
Como foi possível ver, o conceito de tração está muito presente em nosso cotidiano e, apesar de não haver nenhuma fórmula específica para calculá-lo, não existem grandes dificuldades na hora de analisar os casos propostos. Para chegar na prova sem medo de errar, reforce seus conhecimentos com esse conteúdo sobre estática.
Referências
YOUNG, Hugh D. et al. Física I: Mecânica. São Paulo: Addison Wesley, 2008.
NUSSENZVEIG, H. Moysés. Curso de Física Básica 1: Mecânica. Rio de Janeiro: Edgard Blucher, 2002.

Por Hugo Shigueo Tanaka
Divulgador Científico e co-fundador do canal do YouTube Ciência em Si. Historiador da Ciência. Professor de Física e Matemática. Licenciado em Física pela Universidade Estadual de Maringá (UEM). Mestre em Ensino de Ciências e Matemática (PCM-UEM). Doutorando em Ensino de Ciências e Matemática (PCM-UEM).
Tanaka, Hugo Shigueo. Tração. Todo Estudo. Disponível em: https://www.todoestudo.com.br/fisica/tracao. Acesso em: 19 de February de 2026.
1.
Considere o bloco suspenso por um fio ideal (sem massa, com dimensões desprezíveis e inextensível) conforme mostra a figura abaixo:
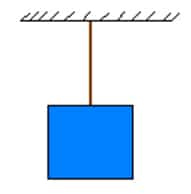
Sabendo que a aceleração da gravidade local é 10 m/s2 e que a massa do bloco é de 2 kg. Determine a força de tração nesse fio.
Para resolver o exercício, fazemos uma análise do caso. É possível perceber que as forças que estão atuando sobre o bloco são as forças de tração (T) e peso (P). Ambas possuem sentidos contrários. Dessa forma, como o sistema está em equilíbrio, obtemos:
T – P = 0.
“Isolando” a tração:
T = P
Sabe-se que a força peso é dada pelo produto da massa do corpo pela aceleração gravitacional no local. Logo, obtemos:
T = mg
Substituindo os valores:
T = 10*2
T = 20 N.
Portanto, a tração no fio é 20 N.
2. [Unesp]
Dois blocos A e B, de massas 2,0 kg e 6,0 kg, respectivamente, e ligados por um fio, estão em repouso sobre um plano horizontal. Quando puxado para a direita pela força F mostrada na figura, o conjunto adquire aceleração de 2,0 m/s2
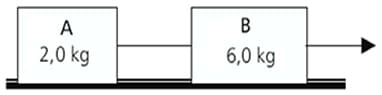
Nestas condições, pode-se afirmar que o módulo da resultante das forças que atuam em A e o módulo da resultante das forças que atuam em B valem, em newtons, respectivamente,
a) 4 e 16
b) 16 e 16
c) 8 e 12
d) 4 e 12
e) 1 e 3
De acordo com a Segunda Lei de Newton, podemos determinar a força resultante que age em cada um dos blocos.
Dessa forma, no bloco A, temos:
FRa = maᐧa
E no bloco B:
FRb = mbᐧa
Substituindo os valores, obtemos que:
FRa = 4N
FRb = 12N
Resposta: D.