Quando estamos em uma viagem de carro, nos deparamos com algumas curvas. Assim que o carro realiza uma curva, sentimos nosso corpo ser “jogado” para o lado. Da mesma forma, um passageiro de um ônibus também sente essa mudança de movimento quando o motorista realiza uma curva pra esquerda ou direita. Isso acontece pela ação da força centrípeta.
Publicidade
Entenda os motivos pelos quais sentimos nosso corpo se mover em sentido contrário ao movimento da curva e veja mais exemplos da aplicação dessa força. Também estudaremos os conceitos de aceleração centrípeta e a existência ou não da força centrífuga.
O que é a força centrípeta?
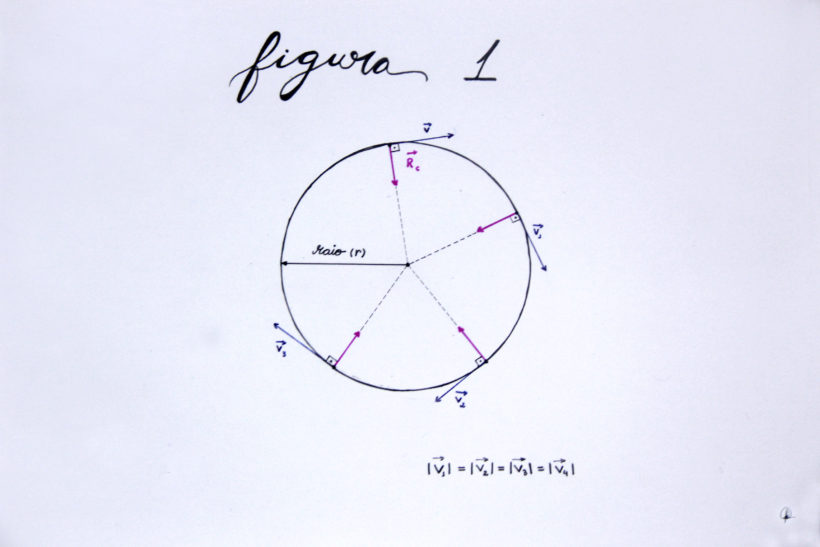
Primeiramente, vamos analisar um determinado corpo em movimento circular uniforme em uma determinada região, conforme a Figura 1:
Relacionadas
Sabe-se que, de acordo com a Primeira Lei de Newton, um corpo permanecerá em repouso ou em movimento uniforme se nenhuma força externa agir sobre ele.
Por outro lado, podemos observar na Figura 1 que o objeto mantém o valor de sua velocidade linear durante todo o trajeto, porém sua direção muda conforme o tempo passa.
Isso significa que existe alguma força que faça com que a direção do objeto seja alterada. Essa força que aponta para o centro da região da circunferência é a chamada força centrípeta.
Segunda Lei de Newton
Conhecida também como “Princípio da Dinâmica”, a segunda lei de Newton se refere a uma força resultante não nula que é aplicada sobre um objeto parado ou em movimento.
Publicidade
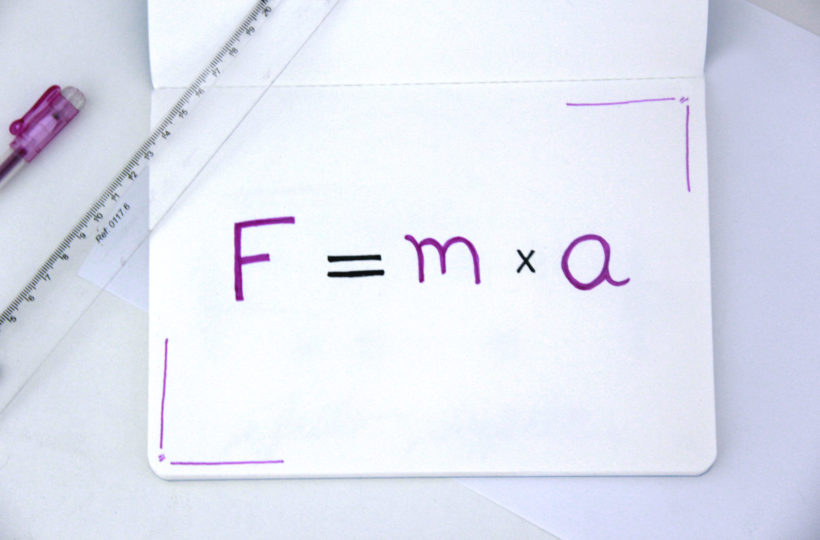
Segundo ela, qualquer variação do vetor velocidade (módulo, direção ou ambos) explica o fato dessa força resultante ser diferente de zero.
Logo, para o movimento circular uniforme, a segunda lei de Newton nos diz que a força centrípeta aponta para o centro. Essa aceleração que aponta para o centro é conhecida como aceleração centrípeta.
Enfim, a equação geral para a força centrípeta, a partir da segunda lei de Newton é:
Publicidade
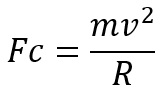
Aceleração centrípeta
A partir da formulação da força centrípeta, aparece uma aceleração, a já mencionada aceleração centrípeta.
Essa aceleração aparece em movimentos circulares uniformes ou não uniformes. Ela aponta para o centro da circunferência.
Tanto em um movimento circular uniforme como em um não uniforme, a aceleração centrípeta altera apenas a direção do movimento do objeto.
A mudança de valor da velocidade está relacionada à aceleração tangencial, assunto para um futuro próximo.
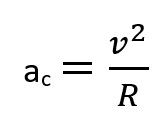
A partir da imagem da equação da aceleração centrípeta, podemos observar que ela é diretamente proporcional ao quadrado da velocidade linear do objeto e inversamente proporcional ao raio da circunferência.
A força centrípeta aparece em muitas situações no nosso dia a dia. Além disso, é importante entender a matemática envolvida por trás dessas explicações qualitativas, para resolvermos exercícios e entendermos exemplos dessas situações.
Força centrífuga
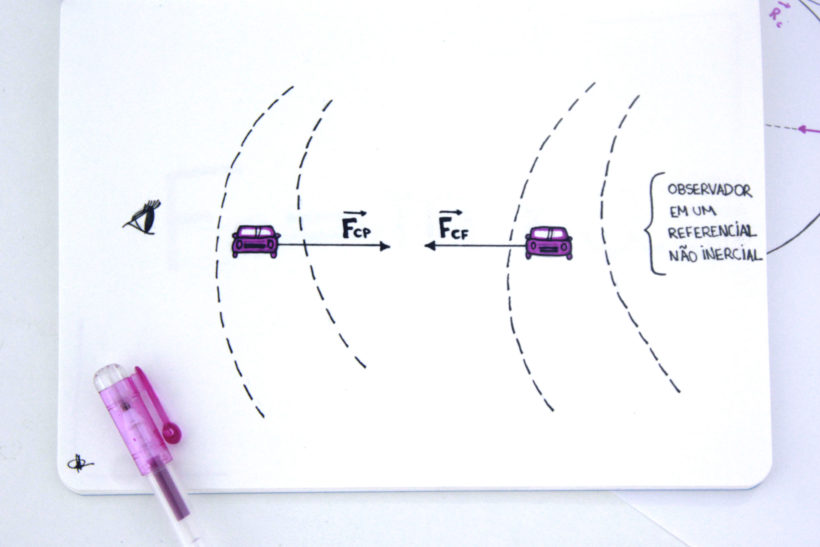
De antemão, vemos na imagem que surge uma força contrária à força centrípeta. Essa força é conhecida como força centrífuga.
Porém, essa força não é detectada nos referenciais inerciais, sendo chamadas de “forças fictícias”.
Um exemplo disso são as gotas que saem das roupas colocadas em uma máquina de lavar.
Como estamos em um referencial inercial (Terra) em relação ao movimento das roupas, a resultante que aparece é a força centrípeta, que faz com que as roupas acompanhem o movimento. Dessa forma, as gotas são ejetadas por inércia para fora do cesto da máquina de lavar roupas.
Em conclusão, a força centrípeta e a centrífuga não formam um par ação-reação, pois são forças consideradas em referenciais distintos.
Entenda mais sobre força centrípeta
Em síntese, podemos utilizar alguns vídeos para melhor entender o conteúdo de força centrípeta.
Teoria sobre a força centrípeta
Neste vídeo, é abordado todo o conteúdo teórico explicado no texto e algumas informações a mais sobre o assunto.
Exercícios resolvidos sobre força centrípeta
Da mesma forma, este vídeo aplica toda a teoria explicada nos exercícios mais comuns de vestibulares.
Entendendo a força centrífuga
Sob o mesmo ponto de vista, podemos entender um pouco melhor a força centrífuga a partir da explicação do vídeo.
Em conclusão, a força centrípeta pode ser analisada de várias formas no nosso cotidiano. Além disso, podemos analisá-la em alguns exercícios de vestibulares ou apenas de uma forma mental, como os exemplos do ônibus e o carro em viagem citados.
Referências
Kazuhito Yamamoto, Física para o ensino médio, vol. 1 : mecânica;
Wilson Carron, As faces da física : volume único.

Por Guilherme Santana da Silva
Graduado no curso de Física pela Universidade Estadual de Maringá. Professor assistente em um colégio de ensino médio e preparatório para os vestibulares. Nas horas vagas se dedica à vida religiosa, praticar mountain bike, tocar bateria, dar atenção à família e cuidar de suas duas gatinhas Penélope e Mel.
Santana, Guilherme. Força Centrípeta. Todo Estudo. Disponível em: https://www.todoestudo.com.br/fisica/forca-centripeta. Acesso em: 14 de February de 2026.
1. [UFMG-MG]
Devido a um congestionamento aéreo, o avião em que Flávia viajava permaneceu voando em uma trajetória horizontal e circular, com velocidade de módulo constante.
Considerando-se essas informações, é CORRETO afirmar que, em certo ponto da trajetória, a resultante das forças que atuam no avião é
A) horizontal.
B) vertical, para baixo.
C) vertical, para cima.
D) nula.
Como a curva é horizontal, a força resultante centrípeta que é radial e dirigida para o centro da circunferência deverá ser também horizontal.
RESPOSTA: A
2. [UFSM-RS]
A figura representa dois atletas numa corrida, percorrendo uma curva circular, cada um em uma raia.

Eles desenvolvem velocidades lineares com módulos iguais e constantes, num referencial fixo no solo. Atendendo à informação dada, assinale a resposta correta.
A) Em modulo, a aceleração centrípeta de A é maior do que a aceleração centrípeta de B.
B) Em modulo, as velocidades angulares de A e B são iguais.
C) A poderia acompanhar B se a velocidade angular de A fosse maior do que a de B, em modulo.
D) Se as massas dos corredores são iguais, a força centrípeta sobre B é maior do que a força centrípeta sobre A, em modulo.
E) Se A e B estivessem correndo na mesma raia, as forças centrípetas teriam módulos iguais, independentemente das massas.
Sabemos que a aceleração centrípeta tem a seguinte equação:
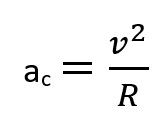
Observa-se que a aceleração centrípeta é inversamente proporcional ao raio de curvatura, ou seja, quanto menor o raio, maior será a aceleração centrípeta de um objeto.
Dessa forma, a aceleração centrípeta de A é maior que a aceleração centrípeta de B.
RESPOSTA: A