Desenvolvida por Émile Clapeyron (1799-1864), a equação que leva o seu nome relaciona as três variáveis de estados dos gases: pressão, temperatura e volume. Ela é relacionada ao número de partículas (número de mols) de uma amostra de gás. Vamos estudar aqui o que é essa equação, qual a relação dela com a lei geral dos gases e alguns exercícios resolvidos.
Publicidade
Fórmula
Como dito, Clapeyron, em seus estudos, estendeu a lei geral dos gases para uma amostra de gás constítuida de n mols de partículas. Em outras palavras, para 1 mol de partículas em forma de gás, ele descobriu que a expressão da lei geral dos gases sempre mostrava um mesmo valor R, chamada atualmente de constante universal dos gases.
![]()
Relacionadas
Porém, para uma amostra de n mols de partículas, essa expressão acima pode ser representada como sendo a seguinte fórmula, conhecida como equação de Clapeyron:
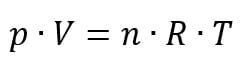
em que:
- p: pressão (atm)
- V: volume (litros)
- n: número de mols (mol)
- R: constante universal dos gases (possui o valor de 0,082 no S.I)
- T: temperatura (Kelvin)
Podemos relacionar essa equação com a lei geral dos gases, que será explicada a seguir.
Publicidade
A lei geral dos gases
A lei geral dos gases perfeitos resume os resultados das três transformações gasosas particulares (Isobárica, isométrica e isotérmica). Ela é expressa da seguinte forma:
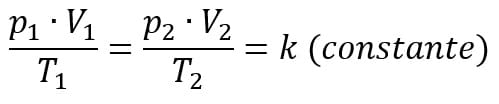
A relação entre a equação de Clapeyron e a lei geral dos gases está no fato de que ambas abordam as três variáveis de estados termodinâmicos. A única diferença é que a primeira relaciona o número de mols de uma certa quantidade de gás e a segunda não.
Publicidade
Vídeos sobre a equação de Clapeyron
Para ilustrar melhor seus estudos, confira vídeos sobre a equação de Clapeyron, com explicações didáticas e aplicações da equação. Confira!
Teoria e exemplos resolvidos
Neste vídeo é apresentado uma breve teoria da equação de Clapeyron e algumas aplicações dessa equação, além de macetes para você aprender de vez a fórmula da equação.
Como surgiu a equação de Clapeyron
Ótimo para entender como Clapeyron chegou à equação que leva seu nome, esse vídeo te dará dicas imperdíveis para aprender esse conteúdo.
Exercícios resolvidos
Pensando nas provas, esse vídeo apresenta alguns exercícios resolvidos sobre a equação de CLapeyron. Dessa forma, você diminui a probabilidade de se enroscar em uma questão sobre o assunto!
Com exemplos e resoluções, ficou muito mais fácil entender a equação, não é mesmo? Estude também Lei dos Gases e entenda tudo sobre eles!
Referências
As faces da física – Wilson Carron e Osvaldo Guimarães.
Física para o ensino médio, volume 2 – Kazuhito Yamamoto e Luiz Felipe Fuke.

Por Guilherme Santana da Silva
Graduado no curso de Física pela Universidade Estadual de Maringá. Professor assistente em um colégio de ensino médio e preparatório para os vestibulares. Nas horas vagas se dedica à vida religiosa, praticar mountain bike, tocar bateria, dar atenção à família e cuidar de suas duas gatinhas Penélope e Mel.
Santana, Guilherme. Equação de Clapeyron. Todo Estudo. Disponível em: https://www.todoestudo.com.br/fisica/equacao-de-clapeyron. Acesso em: 14 de February de 2026.
1. [Mackenzie- SP]
Um recipiente de volume V, totalmente fechado, contém 1 mol de um gás ideal, sob uma certa pressão p. A temperatura absoluta do gás é T e a constante universal dos gases perfeitos é R= 0,082 atm.litro/mol.K. Se esse gás é submetido a uma transformação isotérmica, cujo gráfico está representado abaixo,
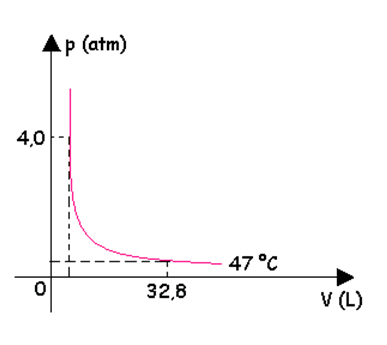
podemos afirmar que a pressão, no instante em que ele ocupa o volume é de 32,8 litros, é:
a) 0,1175 atm
b) 0,5875 atm
c) 0,80 atm
d) 1,175 atm
e) 1,33 atm
No estado final temos V = 32,8 L
Transformando a variação de temperatura Celsius para Kelvin, teremos:
T = θ + 273
T = 47 + 273
T = 320 K
Substituindo na eq. de Clapeyron
pV = nRT
p . 32,8 = 1. 0,082. 320
p = 0,80 atm
RESPOSTA: c)
2. [PUC-SP]
Um certo gás, cuja massa vale 140g, ocupa um volume de 41 litros, sob pressão 2,9 atmosferas a temperatura de 17°C. O número de Avogadro vale 6,02. 1023 e a constante universal dos gases perfeitos R= 0,082 atm.L/mol.K.
Nessas condições, o número de moléculas continuadas no gás é aproximadamente de:
a) 3,00. 1024
b) 5,00. 1023
c) 6,02. 1023
d) 2,00. 1024
e) 3,00. 1029
Substituindo os valores dados na eq. de Clapeyron
pV = nRT
2,9. 41 = n. 0,082. 290
n = 5 mols
Usaremos regra de três simples para calcularmos o valor das moléculas
1 mol _______ 6,02 .1023 moléculas
5 mols ______ x
x ≈ 3,00. 1024 moléculas (note que este é um valor aproximado: houve a utilização da regra de arredondamento.)
RESPOSTA: a)