Durante nossos estudos de matemática, muitas vezes nos deparamos com frases como “essa expressão é maior do que aquela” ou “o valor x é menor do que o valor y“. Isso pode ser encontrado também nas inequações, que são expressões matemáticas que não utilizam o sinal de igual. Entenda o que é uma inequação, como solucionar e veja exercícios resolvidos.
Publicidade
O que é uma inequação
Uma inequação é uma desigualdade que está ligada a alguma variável, muitas vezes sendo em relação à variável x. Ela é muito utilizado em estudos dos sinais das funções, tanto as de 1° grau como as de 2° grau. Por outro lado, também podemos encontrar inequações no nosso cotidiano, como a tabela de índice de massa corporal.
Relacionadas
São utilizados alguns símbolos matemáticos para representá-las. A seguir, mostraremos quais são esses símbolos.
- > (maior que): indica que uma expressão é maior do que outra expressão ou algum número;
- < (menor que): é utilizado quando se quer informar que uma expressão matemática é menor que um número ou outra expressão;
- ≥ (maior ou igual): indica que a inequação que está sendo analisada é maior ou igual a um número ou uma expressão matemática;
- ≤ (menor ou igual): símbolo que informa que uma inequação é menor ou igual a algo;
- ≠ (diferente): indica que uma inequação é diferente de um número ou de alguma expressão.
Anotou todos os símbolos? A seguir, vamos entender o que são inequações de primeiro e segundo grau e como resolvê-las.
Inequação de primeiro grau
Uma inequação do primeiro grau pode ser definida da seguinte forma:
Inequação do 1° grau na variável x é toda desigualdade que pode ser representada como
(ou com as relações >, ≥, ≤ ou ≠), em que a e b são constantes reais, com a≠0.Publicidade
A resolução das inequações de primeiro grau é fundamentada nas propriedades das desigualdades descritas a seguir:
- Se adicionarmos ou subtrairmos um mesmo número de ambos os lados de uma desigualdade, a desigualdade se mantém;
- Dividindo ou multiplicando por um mesmo número positivo ambos os lados de uma desigualdade, ela se mantém a mesma;
- Multiplicando ou dividindo por um mesmo número negativo ambos os membros de uma desigualdade do tipo >, <, ≥ ou ≤, a desigualdade inverte o sentido.
Veja, a seguir, um exemplo de como se resolve uma inequação do primeiro grau:

Publicidade
Inequação de segundo grau
As inequações do segundo grau são as desigualdades que contêm uma expressão matemática do segundo grau, ou seja, a variável a ser estudada deve estar elevada ao quadrado. A forma de uma inequação do segundo grau é representada a seguir:
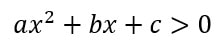
Lembrando que o sinal de “maior”, na expressão acima, pode ser substituído por qualquer um daqueles já apresentados anteriormente. Para resolver esse tipo de inequação, é necessário aplicar Bhaskara. Dessa forma, será possível obter as raízes da expressão e, posteriormente, obter um intervalo em que seja possível a determinação de um conjunto solução para a inequação. A seguir, é apresentado um exemplo de resolução de uma inequação desse tipo:

Vídeos sobre as inequações
Para que você possa compreender melhor as inequações e se dar muito bem nas provas, acompanhe as videoaulas a seguir e continue estudando sobre o assunto!
Inequação do primeiro grau
Aqui, será apresentada uma base teórica para a inequação do primeiro grau, além da explicação dos símbolos utilizados. Na videoaula, você acompanha também a resolução de alguns exercícios.
Exercícios resolvidos
Para que você possa entender melhor como se resolve uma inequação do 1° grau, veja a resolução de exercícios no vídeo!
Inequações do segundo grau
Nesse vídeo, você poderá entender um pouco mais sobre as inequações do 2° grau. Além disso, ele traz exemplos resolvidos dessa inequação.
Para fixar bem o conteúdo, é importante que você revise sobre a fórmula de Bhaskara, equações do primeiro e segundo grau e soma e produto, que é uma forma de resolver as equações de segundo grau. Comece por nosso conteúdo sobre equações de primeiro grau. Assim, seus estudos ficarão completos!
Referências
IEZZI et al. Matemática: ciência e aplicações. Ensino Médio.
DANTE, Luiz Roberto. Matemática: contexto & aplicações. Ensino Médio.

Por Guilherme Santana da Silva
Graduado no curso de Física pela Universidade Estadual de Maringá. Professor assistente em um colégio de ensino médio e preparatório para os vestibulares. Nas horas vagas se dedica à vida religiosa, praticar mountain bike, tocar bateria, dar atenção à família e cuidar de suas duas gatinhas Penélope e Mel.
Santana, Guilherme. Inequação. Todo Estudo. Disponível em: https://www.todoestudo.com.br/matematica/inequacao. Acesso em: 18 de February de 2026.
1.
Quais são os resultados naturais da inequação a seguir?
2x – 18 > 4x – 38
a) x > 10
b) x < 10
c) x = 10
d) x é um número natural
e) x = 0, x = 1, x = 2, x = 3, x = 4, x = 3, x = 5, x = 6, x = 7, x = 8 e x = 9
Vamos somar 18 e subtrair 4x de ambos os lados. Dessa forma:
2x – 18 + 18 – 4x > 4x – 38 + 18 – 4x
2x – 4x > – 38 + 18
-2x > -20
Vamos multiplicar ambos os lados por -1 para alterar o sinal. Ao fazermos isso, o sinal da desigualdade muda para “menor que”, ou seja, muda para <.
Logo:
(-1) –2x > –20 (–1)
2x < 20
Dividindo agora ambos os lados por 2:
2x/2 < 20/2
x < 10
Lembre-se de que os valores naturais menores que 10 são: 0, 1, 2, 3, 4, 5, 6, 7, 8 e 9. O número 10 não é menor que 10, logo, ele não pertence ao conjunto de soluções da inequação.
RESPOSTA: e)
2.
O conjunto solução da inequação (x – 2)² < 2x – 1, considerando como universo o conjunto dos reais, está definido por:
a) 1 < x < 5
b) 3 < x < 5
c) 2 < x < 4
d) 1 < x < 4
e) 2 < x < 5
Solucionando o quadrado da diferença no primeiro membro da inequação, teremos:
(x – 2)² < 2x – 1
x² – 4x + 4 < 2x – 1
x² – 6x + 5 < 0
Vamos utilizar Bhaskara para resolver a inequação. Começamos pelo valor de delta:
Δ = (– 6)² – 4.1.5
Δ = 36 – 20
Δ = 16
Assim, na fórmula de Bhaskara, teremos:
x = – ((– 6) ± √16)/2
x = (6 ± 4)/2
x = 3 ± 2
Logo, as duas possíveis soluções são:
x’ = 5
x” = 1
RESPOSTA: a)