Como contar alguma coisa absurdamente grande? Aqui, você irá entender como é importante o conhecimento da análise combinatória, além de estudar alguns métodos de contagem. No fim, veremos algumas videoaulas para que seu conhecimento aumente mais ainda!
Publicidade
O que é análise combinatória
A análise combinatória é o estudo matemático da contagem. Por exemplo, demoraria 19 quatrilhões de anos para contar, um a um, 602×1021 átomos de alumínio de um cubo cuja aresta mede 3,32 cm. Para viabilizar esse tipo de contagem, entre outros, sçao necessários métodos de contagem para tal tarefa e é justamente isso que a análise combinatória engloba.
Relacionadas
Dessa forma, vamos estudar alguns dessts métodos que são o arranjo, a permutação e a combinação.
Qual a diferença de arranjo, permutação e combinação?
Os métodos de contagem são de extrema importância na análise combinatória. São eles que nos auxiliam na contagem de determinadas situações que seriam impossíveis – ou quase impossível – de se contar na mão. Com isso, em mente, vamos então entender um pouco mais sobre eles.
Arranjo simples
Arranjo é um agrupamento em que a ordem deve ser considerada. Por exemplo, a palavra LAGO é um arranjo de letras, pois se trocarmos as letras de lugares podemos obter outra palavra como a palavra GALO.
Para calcularmos um arranjo, antes de mais nada, vamos ver uma definição formal do que seria um arranjo simples.
Publicidade
Seja I={a1,a2,a3,…,an} um conjunto formado por n elementos e p um número natural tal que p≤n. Chama-se arranjo simples de p elementos de I toda sequência formada por p elementos distintos de I.
Dessa forma, podemos calcular arranjos simples de duas maneiras: por meio do princípio fundamental de contagem ou por fatorial. Vamos primeiro ver a fórmula utilizando o princípio fundamental de contagem.
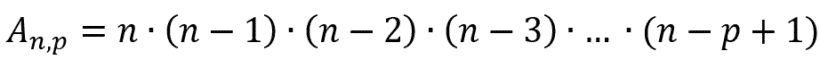
Publicidade
Sendo que An,p é o número de arranjos simples dos n elementos do conjunto analisado tomados p a p. Utilizando fatorial, teremos a seguinte fórmula:
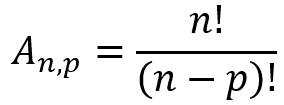
Permutação
A permutação é um caso isolado dos arranjos simples, pois aqui é possível a repetição de elementos de um conjunto em uma contagem tendo apenas a troca de lugar desse elemento. Por exemplo, seja o conjunto I = {a,b,c}. Se fizermos a permutação deste conjunto, tomando 3 a 3 destes elementos, teremos a seguinte situação:
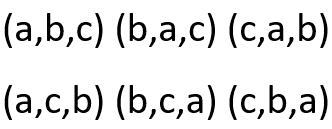
Observe que duas destas permutações de diferem apenas pela ordem dos elementos. Uma definição formal da permutação seria a seguinte:
Seja I={a1,a2,a3,…,an} um conjunto formado por n elementos. Chama-se permutação simples dos n elementos de I todo arranjo simples desses n elementos tomados n.
Podemos calcular uma permutação simples da seguinte forma:
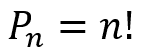
Combinação
A combinação simples pode ser considerada agrupamento de elementos de um conjunto em subconjuntos. Uma definição formal seria a seguinte:
Seja I={a1,a2,a3,…,an} um conjunto formado por n elementos e p um número natural tal que p≤n. Chama-se combinação simples de p elementos de I todo subconjunto de I formado por p.
Podemos calcular uma combinação simples da seguinte maneira:
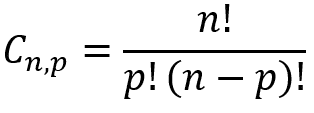
em que Cn,p é o número de combinações simples possíveis de um conjunto I.
Para finalizarmos, vamos assistir algumas videoaulas para que o assunto estudado até aqui possa ficar sem perguntas e dúvidas!
Saiba mais sobre análise combinatória
Apresentaremos a seguir algumas videoaulas sobre análise combinatória para que você possa entender muito mais sobre esse conteúdo e tirar suas dúvidas restantes sobre o assunto!
Principio fundamental da contagem
Neste primeiro vídeo, vamos entender um pouco mais sobre o que realmente é o princípio fundamental da contagem!
Arranjo, permutação e combinação
Entenda aqui os três métodos de contagem para que você possa se dar muito bem nas provas!
Exercícios resolvidos
Ver a teoria na prática sempre nos auxilia muito na hora de resolver exercícios. Dessa forma, apresentamos aqui uma videoaula de resolução de exercícios que são voltados para os vestibulares!
Por fim, para que seus estudos possam ficar completos, é importante revisar sobre o conteúdo de conjuntos!
Referências
IEZZI et al. Matemática: ciência e aplicações. Ensino Médio.
DANTE, Luiz Roberto. Matemática: contexto & aplicações. Ensino Médio.

Por Guilherme Santana da Silva
Graduado no curso de Física pela Universidade Estadual de Maringá. Professor assistente em um colégio de ensino médio e preparatório para os vestibulares. Nas horas vagas se dedica à vida religiosa, praticar mountain bike, tocar bateria, dar atenção à família e cuidar de suas duas gatinhas Penélope e Mel.
Santana, Guilherme. Análise combinatória. Todo Estudo. Disponível em: https://www.todoestudo.com.br/matematica/analise-combinatoria. Acesso em: 17 de February de 2026.
1. [UFOP-MG]
No meio da “invasão tecnológica” que toma conta de nossas vidas, dona Antônia esqueceu sua senha bancária justamente na hora de efetuar um saque. Ela lembra que a senha é formada por quatro algarismos distintos, sendo o primeiro 5 e o algarismo 6 aparece em alguma outra posição.
Qual é o número máximo de tentativas que o banco deveria permitir para que dona Antônia consiga realizar o saque?
Aqui precisamos usar o conceito de arranjos, pois a senha 5123 é diferente da senha 5321.
Como o número 5 estará sempre em uma das combinações e o número 6 nas outras possibilidades, teremos 3 vezes a possibilidade de um arranjo do tipo A8,2. Dessa forma, teremos
A8,2 + A8,2 + A8,2 = 3∙A8,2
Lembrando que o arranjo simples é calculado a partir da seguinte fórmula
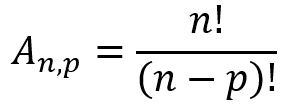
Portanto, teremos que o número máximo de tentativas é
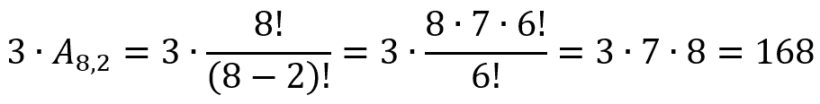
2.
Júlia deseja viajar e levar 5 pares de sapatos, sabendo que ela possui em seu guarda-roupa 12 pares, de quantas maneiras diferentes Júlia poderá escolher 5 pares de sapatos para a sua viagem?
Se Júlia leva o sapato preto e o sapato rosa, é a mesma coisa que ela levar o sapato rosa e o sapato preto, logo, a sequência dos elementos não importa, com isso usaremos Combinação, para eliminarmos os arranjos repetidos.
Usando a fórmula para combinação, teremos que
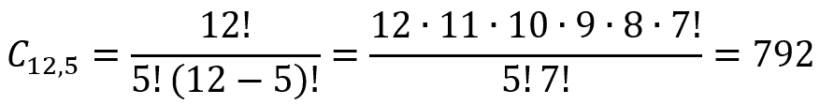
Ela poderá escolher 792 combinações.