Na construção civil, para a prevenção contra possíveis trincas ou rupturas, utilizam-se “folgas”. Mas qual o motivo da utilização dessas “folgas”? Isso é explicado pela dilatação linear. Dessa forma, estudaremos aqui o que é essaa dilatação, a sua equação, o coeficiente e a diferença entre dilatação superficial e volumétrica.
Publicidade
O que é e como calcular a dilatação linear?
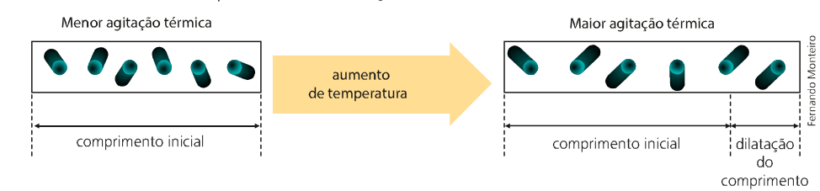
Podemos dizer, de modo geral, que todos os corpos possuem uma variação em suas dimensões quando se aquecem ou se resfriam, e é essa variação de dimensões que chamamos de dilatação. Em geral, quando se eleva a temperatura de um corpo suas partículas aumentam a agitação térmica, causando assim um aumento relativo entre elas.
Relacionadas
Porém, em alguns casos podemos considerar apenas uma dimensão (comprimento), como por exemplo os trilhos de uma estrada de ferro. Nessas situações chamamos essa dilatação de dilatação linear. Assim, iremos entender como se calcula essa dilatação.
Cálculo e equação
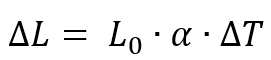
- ΔL: variação do comprimento;
- L0: comprimento inicial;
- α: coeficiente de dilatação linear;
- ΔT: variação da temperatura.
A dilatação pode ser dita então como sendo diretamente proporcional ao comprimento inicial (L0), diretamente proporcional à variação de temperatura (ΔT = T – T0) e depende do tipo de material (α).
Coeficientes de dilatação linear
Como dito acima que a dilatação linear depende do material, iremos apresentar a seguir uma tabela com alguns materiais e seus respectivos coeficientes.
Publicidade
| Material | Coeficiente de Dilatação (°C-1) |
|---|---|
| Porcelana | 3.10-6 |
| Vidro pirex | 3.10-6 |
| Vidro comum | 8.10-6 |
| Platina | 9.10-6 |
| Aço | 11.10-6 |
| Ferro | 12.10-6 |
| Cobre | 17.10-6 |
| Latão | 19.10-6 |
| Alumínio | 22.10-6 |
| Zinco | 26.10-6 |
| Chumbo | 27.10-6 |
Dilatação superficial x volumétrica
A dilatação superficial ocorre quando consideramos, além da dilatação do comprimento, também na dilatação da largura. Assim, a dilatação térmica superficial se refere à variação da área. Um exemplo disso seria em placas de concreto.
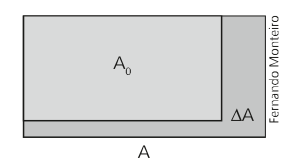
Podemos pensar na dilatação volumétrica do mesmo modo, porém temos que considerar as três dimensões de um corpo, ou seja, o seu comprimento, largura e altura. Assim, a dilatação volumétrica esta relacionada ao volume de um corpo.
Publicidade

Além dessas duas diferenças, temos que considerar também os coeficientes de dilatação superficial e volumétrica. O primeiro é duas vezes maior que o coeficiente de dilatação linear (β = 2α) enquanto o segundo é três vezes maior que o coeficiente de dilatação linear (γ = 3α).
Videoaulas sobre dilatação linear
Por fim, confira alguns vídeos para te auxiliar em um melhor entendimento sobre o assunto estudado até aqui.
Conceitos da dilatação linear
Revise e entenda mais sobre os conceitos dessa dilatação. Dessa forma você garante que nenhuma duvida tenha ficado para trás.
Aprofundamento sobre os conceitos de dilatação linear
Nesse vídeo é apresentado um pouco mais sobre os conceitos, assim você consegue fixar mais ainda o conteúdo.
Exercícios resolvidos
Exercícios resolvidos são muito importantes para a compreensão de como aplicar a equação desse conteúdo na hora da prova.
E falando em prova, a seguir você pode encontrar alguns exercícios sobre dilatação linear para testar seus conhecimentos. Bons estudos!
Referências
Física para o ensino médio, vol. 2: mecânica – Kazuhito Yamamoto;
As faces da física – Wilson Carron.

Por Guilherme Santana da Silva
Graduado no curso de Física pela Universidade Estadual de Maringá. Professor assistente em um colégio de ensino médio e preparatório para os vestibulares. Nas horas vagas se dedica à vida religiosa, praticar mountain bike, tocar bateria, dar atenção à família e cuidar de suas duas gatinhas Penélope e Mel.
Santana, Guilherme. Dilatação Linear. Todo Estudo. Disponível em: https://www.todoestudo.com.br/fisica/dilatacao-linear. Acesso em: 14 de February de 2026.
1. [UDESC/2012]
Em um dia típico de verão utiliza-se uma régua metálica para medir o comprimento de um lápis. Após medir esse comprimento, coloca-se a régua metálica no congelador a uma temperatura de -10ºC e esperam-se cerca de 15 min para, novamente, medir o comprimento do mesmo lápis. O comprimento medido nesta situação, com relação ao medido anteriormente, será:
a) maior, porque a régua sofreu uma contração.
b) menor, porque a régua sofreu uma dilatação.
c) maior, porque a régua se expandiu.
d) menor, porque a régua se contraiu.
e) o mesmo, porque o comprimento do lápis não se alterou.
Ao colocar a régua dentro do congelador, ela sofre uma contração em seu comprimento. Ao medir o lápis com essa régua, o comprimento será maior do que o medido anteriormente.
RESPOSTA: a)
2. [UFLA-95]
Uma barra de ferro homogênea é aquecida de 10°C até 60°C. Sabendo-se que a barra a 10°C tem um comprimento igual a 5 m e que o coeficiente da dilatação linear do ferro é igual 1,2 x 10-6 °C-1, podemos afirmar que a variação de dilatação ocorrida e o comprimento final da barra foram de:
a)5×10-4m; 5,0005m
b)2×10-4m; 5,0002m
c)4×10-4m; 5,0004m
d)3×10-4m; 5,0003m
e)6×10-4; 5,0006m
Temos que o comprimento inicial é de 5m, a variação de temperatura é de 50° (ΔT = 60 – 10) e o coeficiente de dilatação linear é α = 1,2 x 10-6 °C-1.
Dessa forma, utilizando a equação de dilatação linear, temos que
∆L= L0∙α∙∆T
∆L = 5 ∙ 1,2 x 10-6 ∙ 50
∆L = 3.10-4m
O comprimento final é dado pela soma do comprimento inicial juntamente com a dilatação. Assim,
L = L0 + ∆L
L = 5 + 3.10-4
L = 5,0003m
RESPOSTA: d)