Coeficiente de atrito é um coeficiente adimensional que é oposto ao deslizamento de duas superfícies, as quais estão em contato. Assim, podem existir dois tipos de coeficientes de atrito: o estático e o dinâmico. Ou seja, um diz respeito aos corpos em repouso e e o outro ao movimento relativo, respectivamente.
Publicidade
O que é coeficiente de atrito
Coeficiente de atrito é um coeficiente que não possui unidade de medida. Ou seja, é adimensional. Esse coeficiente indica como diferentes superfícies podem se opor ao deslizamento.
Relacionadas

Os coeficientes de atrito são indicados pela letra grega μ (mi). Além disso, esses coeficientes são específicos para cada par de materiais. Isto é, o atrito dependerá dos materiais que estão interagindo e, também, se os corpos estão em repouso ou em movimento relativo.
Coeficiente de atrito estático
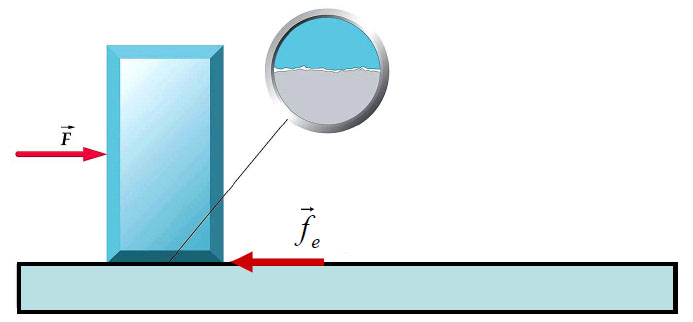
Quando os corpos estão parados entre si, assumimos que há o atrito estático. Ou seja, o μe.
Coeficiente de atrito cinético

Quando os corpos estão em movimento relativo, há o atrito dinâmico. Isto é, o μd
Publicidade
Note que o atrito dinâmico é sempre menor que o atrito estático. Além disso, como trata-se de um coeficiente, seu valor está sempre entre 0 e 1. Dessa forma, 0 é uma condição na qual não há atrito e 1 é uma condição limite, na qual não há movimento.
Como calcular o coeficiente de atrito
Imagine uma situação na qual uma pessoa tenta movimentar um móvel muito grande. Quanto maior for o peso do objeto, maior será a força necessária para deslocá-lo. Além disso, o contato do móvel com o solo também resistirá ao movimento devido ao atrito.

Publicidade
Os cálculos dos coeficientes de atritos são feitos usando a força de atrito. Dessa maneira, matematicamente, temos:
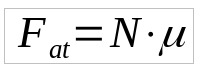
- Fat: Força de atrito (N)
- N: Força normal (N)
- μ: coeficiente de atrito
Note que μ não tem unidade de medida. Além disso, caso o corpo que está sob a ação da força esteja em repouso, usa-se o atrito estático. Porém, se há movimento, usa-se o atrito dinâmico.
Coeficiente de atrito em um plano inclinado
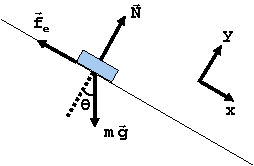
Em um plano inclinado, o cálculo do atrito dependerá do ângulo de inclinação. Dessa maneira, a fórmula será:
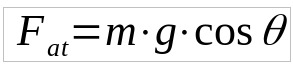
- Fat: Força de atrito (N)
- m: massa (kg)
- g: aceleração da gravidade (m/s2)
- μ: coeficiente de atrito
- cos θ cosseno do ângulo de inclinação
Caso o corpo esteja em repouso no plano inclinado, a força resultante será nula. Porém, caso haja movimento, a força resultante será diferente de zero.
Tabela do coeficiente de atrito
Os coeficientes de atrito são específicos para dois pares de superfícies. Logo, as combinações de materiais que podem entrar em contato são praticamente infinitas. Dessa maneira, veja algumas das principais combinações:
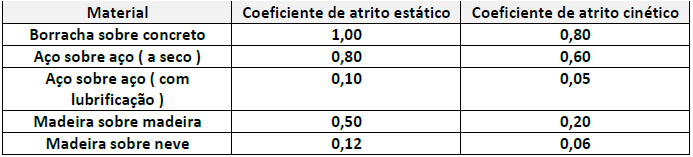
Note que os valores se modificam devido às condições da superfície. Por exemplo, se estão secas ou lubrificadas. Além disso, é importante perceber como os coeficientes de atrito estático são sempre maiores que os coeficientes de atrito dinâmico.
Vídeos sobre coeficiente de atrito
Veja alguns vídeos selecionados sobre os coeficientes de atrito. Assim, você poderá aprofundar ainda mais seus conhecimentos. Confira:
Força de atrito estático
Como calcular a força de atrito quando os corpos estão em repouso? Isso é explicado no vídeo do professor Marcelo Boaro sobre o atrito estático. Ao fim da vídeoaula, Boaro resolve um exercício de aplicação.
Plano inclinado com atrito
O plano inclinado é um caso muito cobrado em provas de grande escala como vestibulares e Enem. Isso acontece porque ele engloba vários conhecimentos de diversas áreas da Mecânica. Por conta disso, o professor Boaro explica como calcular todas as equações que estão envolvidas em um plano inclinado com atrito.
Experimento sobre coeficiente de atrito
O professor Biga faz um experimento que mostra como descobrir o coeficiente de atrito na prática. Durante o vídeo, o docente também explica os conceitos de atrito estático e de atrito dinâmico.
O coeficiente de atrito, bem como a força de atrito são aplicações diretas das Leis de Newton..
Referências
YOUNG, H. D. Física I: Mecânica. São Paulo: Addison & Wesley. 2016.

Por Hugo Shigueo Tanaka
Divulgador Científico e co-fundador do canal do YouTube Ciência em Si. Historiador da Ciência. Professor de Física e Matemática. Licenciado em Física pela Universidade Estadual de Maringá (UEM). Mestre em Ensino de Ciências e Matemática (PCM-UEM). Doutorando em Ensino de Ciências e Matemática (PCM-UEM).
Tanaka, Hugo Shigueo. Coeficiente de atrito. Todo Estudo. Disponível em: https://www.todoestudo.com.br/fisica/coeficiente-de-atrito. Acesso em: 07 de February de 2026.
1. [Udesc]
O gráfico a seguir representa a força de atrito (fat) entre um cubo de borracha de 100 g e uma superfície horizontal de concreto, quando uma força externa é aplicada ao cubo de borracha.
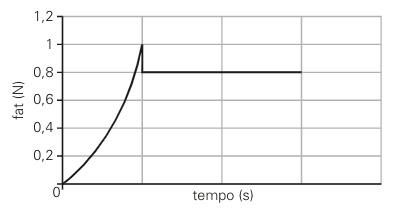
Assinale a alternativa correta, em relação à situação descrita pelo gráfico.
a) O coeficiente de atrito cinético é 0,8.
b) Não há movimento relativo entre o cubo e a superfície antes que a força de atrito alcance o valor de 1,0 N.
c) O coeficiente de atrito estático é 0,8.
d) O coeficiente de atrito cinético é 1,0.
e) Há movimento relativo entre o cubo e a superfície para qualquer valor da força de atrito.
Alternativa correta: A
A linha horizontal do gráfico representa o momento no qual o cubo de borracha está em movimento. Desse modo, a linha horizontal representa o coeficiente de atrito cinético, o qual é igual a 0,8.
2. [Enem]
Uma pessoa necessita da força de atrito em seus pés para se deslocar sobre uma superfície. Logo, uma pessoa que sobe uma rampa em linha reta será auxiliada pela força de atrito exercida pelo chão em seus pés.
Em relação ao movimento dessa pessoa, quais são a direção e o sentido da força de atrito mencionada no texto?
a) Perpendicular ao plano e no mesmo sentido do movimento.
b) Paralelo ao plano e no sentido contrário ao movimento.
c) Paralelo ao plano e no mesmo sentido do movimento.
d) Horizontal e no mesmo sentido do movimento.
e) Vertical e sentido para cima.
Alternativa correta: C
Quando a pessoa anda, ela aplica no solo uma força de atrito horizontal para trás. Pela terceira lei de Newton, o solo aplica nos pés da pessoa uma reação para a frente, no mesmo sentido do movimento, e paralela ao solo.