Graças ao entendimento sobre o que é um campo elétrico, foi possível o desenvolvimento de várias tecnologias em várias áreas como a engenharia, informática e medicina. Desta forma, conheça aqui o que é um campo elétrico, exemplos, além de como calcular, o vetor campo elétrico, as linhas de força, o campo elétrico uniforme, o potencial elétrico e a diferença entre o campo elétrico e a força elétrica.
Publicidade
O que é o campo elétrico
Podemos dizer que o conceito de campo elétrico é análogo ao de um campo gravitacional. Em outras palavras, não podemos vê-lo nem tocá-lo, porém podemos comprovar sua existência usando um corpo de prova. Todo campo é gerado por algum corpo. Por exemplo, o campo gravitacional é gerado por algum planeta ou estrela e age sobre corpos menores ao redor.
Relacionadas
O campo elétrico é gerado por uma carga que chamamos de carga fonte. Para provarmos sua existência, uma carga de prova é colocada no entorno da carga fonte. Assim, iremos perceber que esta carga de prova fica sujeita a uma força elétrica, movendo a carga de prova. Vamos ver algumas aplicações do campo elétrico no nosso dia a dia com dois exemplos a seguir.
Exemplos
- Eletroforese: técnica de separação de moléculas, principalmente em exames de sangue que utiliza um campo elétrico para separar essas moléculas;
- Eletrocardiograma: esse exame detecta o estado do coração pela análise de variação de grandezas elétricas na atividade cardíaca.
A seguir, iremos entender como é feito o cálculo do campo elétrico.
Como calcular
Vimos que uma carga de prova se movimenta ao ser colocada em uma região de um campo elétrico gerado por uma carga fonte. Isso ocorre, pois a carga de prova fica sujeita às forças elétricas de intensidades diferentes. Podemos, então, calcular o campo elétrico a partir da seguinte fórmula, em módulo
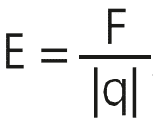
Publicidade
em que:
- E: é o valor do campo elétrico (N/C);
- F: força elétrica que age sobre a carga de prova (N);
- q: carga de prova (C);
Como a força é vetorial e a carga de prova é escalar, logo, o campo elétrico é uma grandeza vetorial. Na fórmula anterior, usamos apenas o módulo, ou seja, os valores absolutos das grandezas vetoriais. Vamos agora entender como seria o vetor campo elétrico.
Vetor campo elétrico
Todo vetor possui direção, sentido e módulo. O campo elétrico, sendo um vetor, também possui essas características. Entretanto, essas características dependem da carga fonte e da carga de teste. Vamos considerar uma carga fonte Q e uma carga de prova q. Se as duas cargas forem positivas (Q>t e q>0), teremos a seguinte situação:
Publicidade
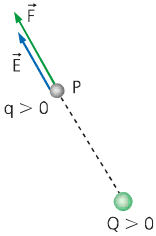
Em outras palavras, o vetor campo elétrico possui a mesma direção e sentido do vetor força elétrica.
No caso em que a carga fonte é positiva (Q>0) e a carga de prova é negativa (q<0), o vetor campo elétrico possui mesma direção, mas em sentido contrário ao da força elétrica e aponta para fora, como pode ser visto na imagem a seguir.
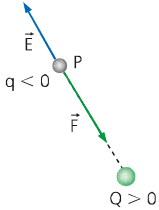
Quando tanto a carga Q como a carga q são negativas, o vetor campo elétrico tem a mesma direção do vetor força elétrica, mas em sentido contrário. A diferença deste caso para o anterior é que, aqui, o vetor campo elétrico aponta na direção da carga fonte.
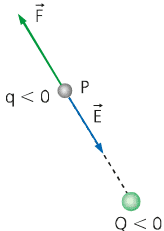
O último caso temos que a carga fonte Q é negativa e a carga q é positiva. Aqui, o vetor campo elétrico possui o mesmo sentido e direção do vetor força. Ambos apontam para a carga fonte.
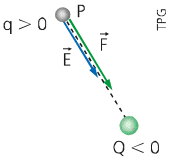
É possível observar que, dependendo do sinal da carga fonte – se ela é positiva ou negativa-, o vetor campo elétrico “sai” desta carga ou “entra” nela. Isto é conhecido como linhas de força de um campo elétrico gerado por uma carga. Desta forma, vamos entender agora o que são estas linhas de força.
Linhas de força
As linhas de forças são linhas imaginárias que tangenciam os vetores campo elétrico em cada ponto e são orientadas no sentido desses vetores.
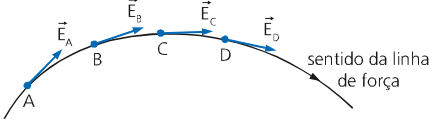
Podemos encontrar três casos para as cargas puntiformes:
Cargas isoladas: as linhas de forças são radiais;
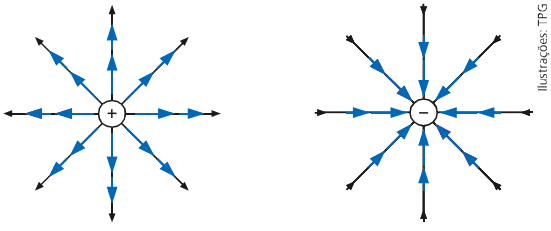
Duas cargas positivas de mesmo módulo: no ponto médio do segmento de reta que liga às duas cargas, o campo elétrico é nulo;
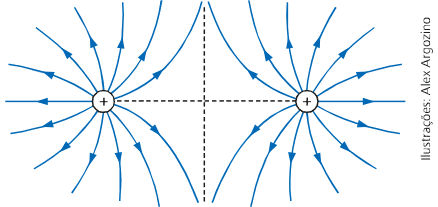
Duas cargas de sinais opostos e de mesmo módulo: as linhas de força saem da carga positiva e entram na carga negativa.
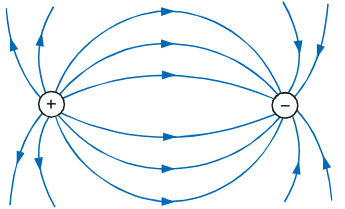
Campo elétrico uniforme
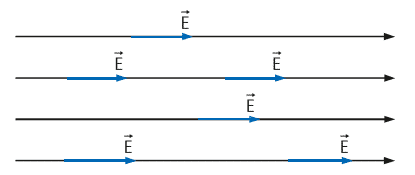
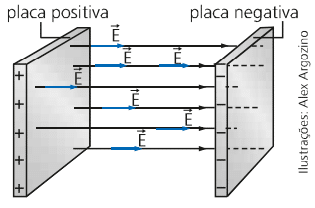
Quando uma região possui todos os campos elétricos na mesma direção, sentido e com o mesmo módulo, dizemos que esta região possui um campo elétrico uniforme. Isso pode ser observado na imagem acima. Um campo desse tipo pode ser gerado por duas placas paralelas carregadas com sinais contrários. A imagem a seguir mostra um exemplo disso.
Campo elétrico e o potencial elétrico
O potencial elétrico é a energia potencial elétrica por unidade de carga. Em outras palavras, podemos escrever isso da seguinte forma:
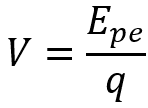
A relação entre campo elétrico e potencial elétrico se deve ao fato da energia potencial elétrica. Isso ocorre pelo fato de que um campo elétrico modifica a velocidade de uma carga de prova e acarreta na modificação de sua energia potencial. Porém, é conveniente trabalharmos com o potencial elétrico (V) e não somente com a energia potencial elétrica.
Campo elétrico X força elétrica
A força elétrica se deve ao fato da interação entre duas cargas. Já o campo elétrico é criado por apenas uma carga e não precisa de uma segunda para existir.
Vídeos sobre campo elétrico
Para que seus estudos possam render muito mais, apresentamos a seguir algumas videoaulas. Dessa forma, qualquer dúvida que tenha ficado para trás será sanada.
Conceitos básicos sobre campo elétrico
Este vídeo apresenta os conceitos básicos de campo elétrico e uma pequena introdução sobre linhas de forças!
Campo elétrico uniforme
Aqui, você pode entender um pouco mais sobre o que é um campo elétrico uniforme para poder se dar muito bem em todas as provas!
Exercícios resolvidos
Ver a teoria na prática é sempre importante. Pensando nisso, apresentamos esse vídeo com alguns exercícios resolvidos!
Por fim é importante revisar os conteúdos sobre carga elétrica, lei de Coulomb e potencial elétrico. Desta forma, seus estudos serão ainda mais completos!
Referências
As faces da física – Wilson Carron e Osvaldo Guimarães.
Física para o ensino médio, volume 3 – Kazuhito Yamamoto e Luiz Felipe Fuke.

Por Guilherme Santana da Silva
Graduado no curso de Física pela Universidade Estadual de Maringá. Professor assistente em um colégio de ensino médio e preparatório para os vestibulares. Nas horas vagas se dedica à vida religiosa, praticar mountain bike, tocar bateria, dar atenção à família e cuidar de suas duas gatinhas Penélope e Mel.
Santana, Guilherme. Campo elétrico. Todo Estudo. Disponível em: https://www.todoestudo.com.br/fisica/campo-eletrico. Acesso em: 09 de February de 2026.
1.
Em um ponto P, onde o vetor campo elétrico tem
direção horizontal e sentido apontado para o oeste, é
colocada uma carga puntiforme de módulo 0,5 µC. Então, essa carga fica sujeita a uma força elétrica de intensidade 0,5 N, na direção horizontal e sentido leste. Nessas condições, determine o módulo do vetor campo
elétrico e o sinal da carga puntiforme.
Como os vetores campo elétrico e da força elétrica são opostos entre si (sentido contrário) e estão na direção horizontal, então podemos concluir que a carga elétrica é negativa.
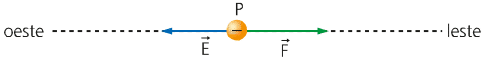
Sabemos que o campo elétrico pode ser calculado pela seguinte fórmula: E = F/q
Temos que F = 0,5N e q = 0,5.10-6C. Assim
E = 0,5/(0,5.10-6)
E = 106N/C
2.
Um ponto material de massa 1 mg (miligrama) eletrizado com carga +2 µC é abandonado no interior de
um campo elétrico uniforme de intensidade 8 • 104 N/C.
Desprezando a ação da força gravitacional, determine:
a) o módulo da força elétrica que atua na carga;
b) a aceleração que a carga adquire;
c) o instante em que o ponto material possui velocidade
de 320 m/s e a distância percorrida por ele nesse
intervalo de tempo.
a)Sabemos que F = qE. Assim
F = 2.10-6• 8.104
F = 0,16N
b)Como a força é constante, podemos utilizar a segunda lei de Newton F = m•a, assim
0,16 = 10-6•a
a = 1,6•105 m/s²
c)Utilizando a equação da velocidade do M.R.U.V, temos
V = V0 + at
320 = 0 + 1,6.105•t
t = 2•10-3s
A distância percorrida nesse tempo é
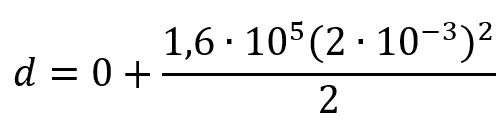
Portanto, a distância percorrida é
d = 0,32m