Razão e proporção são conceitos matemáticos que estão diretamente ligados. Razão representa uma comparação entre duas grandezas. Já a proporção é a comparação entre duas ou mais razões. Nesse post você entenderá o que é razão, o que é proporção e também verá exemplos.
Publicidade
O que é razão
A razão é usada quando queremos comparar dois valores de uma mesma grandeza. Dessa forma, geralmente a razão é expressa como uma divisão. Ou seja, a razão entre dois números a e b é dada como “a para b”, a:b ou a/b. Portanto, a razão pode representar quantas vezes o primeiro número contém o segundo.
O que é proporção
Quando há a igualdade entre duas razões, podemos encontrar a proporção entre elas. Ou seja, se duas razões possuem o mesmo resultado, então, elas são proporcionais. Dessa forma, se a razão entre os números a e b for igual à razão entre os números c e d, teremos que a/b = c/d, que é uma proporção.
Relacionadas
Exemplos de razão e proporção
Razão e proporção são conceitos matemáticos muito utilizados em diversas áreas do conhecimento. Desde a contabilidade até nas ciências naturais, como Física, Química e Biologia.
Porcentagem
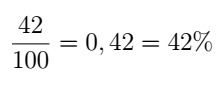
Uma das aplicações do conceito de razão é no cálculo da porcentagem. Assim, toda porcentagem é uma razão com denominador 100. No caso da fração acima, a razão entre os números 42 e 100 é 0,42. Ou seja, 42% de alguma quantidade equivale a 0,42 da mesma quantidade.
Regra de três
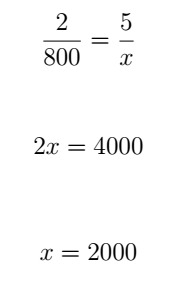
Publicidade
Quanto temos uma proporção e conhecemos três dos quatro valores, podemos encontrar o quarto valor a partir da resolução de uma regra de três. Nesse caso, usamos a propriedade da proporção na qual o produto entre os extremos é igual ao produto entre os meios, ou seja, multiplicamos cruzado. Dessa forma, é possível encontrar o valor de x.
Para o cálculo da razão é necessário notar que ambas as grandezas devem possuir a mesma unidade de medida. Já no cálculo da proporção, é necessário verificar qual a relação de proporção entre as grandezas: diretamente proporcionais ou inversamente proporcionais.
Vídeos sobre Razão e Proporção.
Separamos alguns vídeos para você aprofundar seus conhecimentos sobre razão e proporção. Confira!
Publicidade
Razão e proporção
Nesse vídeo a Professora Angela explica os conceitos de razão e proporção de maneira acessível. A videoaula é ótima para inicar os estudos de razão e proporção.
Proporcionalidade
Para aprofundar ainda mais seus estudos nos conceitos de razão e proporção, assista ao vídeo do prof. Rafael Procópio. Nessa aula, o professor abordará os conceitos de razão e proporção, que é um dos conteúdos mais cobrados na prova de Matemática do Enem.
Regra de três
A regra de três é uma das contas mais importantes da matemática. Então, Iberê Thenório explica de maneira lúdica como é possível aplicar esse conceito em diversas ocasiões do nosso cotidiano.
Agora que você já aprendeu o que é razão e proporção, é hora de aplicar esse conhecimento. Por isso, confira nosso post sobre Regra de Três Simples e Composta.
Referências
SCHWERTL, S. L. Matemática Básica. Blumenau: Edifurb. 2012.

Por Hugo Shigueo Tanaka
Divulgador Científico e co-fundador do canal do YouTube Ciência em Si. Historiador da Ciência. Professor de Física e Matemática. Licenciado em Física pela Universidade Estadual de Maringá (UEM). Mestre em Ensino de Ciências e Matemática (PCM-UEM). Doutorando em Ensino de Ciências e Matemática (PCM-UEM).
Tanaka, Hugo Shigueo. Razão e proporção. Todo Estudo. Disponível em: https://www.todoestudo.com.br/matematica/razao-e-proporcao. Acesso em: 05 de February de 2026.
1. [UERJ]
Admita que, em dezembro de 2014, uma filha tinha 20 anos e seu pai, 50. Em dezembro de 2024, a razão entre as idades da filha e do pai será de:
a) 1/5
b) 1/2
c) 3/4
d) 4/3
Após 10 anos, as idades dos dois serão iguais a 30 anos e 60 anos, respectivamente. Logo, a resposta é dada por
30/60 = 1/2.
Alternativa correta: B
2. [UFPR]
No ano de 2018, a densidade populacional da cidade de Curitiba foi estimada em 4.406,96 habitantes por quilômetro quadrado. Supondo que a área territorial da cidade seja de 435km2, o número que mais se aproxima da população estimada de Curitiba em 2018 é:
a) 1.916.610
b) 1.916.760
c) 1.917.027
d) 1.917.045
e) 1.917.230.
A densidade demográfica de uma região é a razão entre a população e a área da região. Dessa forma, a resposta correta é obtida pela multiplicação da densidade populacional pela área da cidade.
Assim:
4406,96 * 435 ≅ 1917027
Alternativa correta: C