Chamamos de radiciação a operação matemática envolvendo o produto a partir de uma multiplicação, onde os fatores são iguais em seu fundamento. Quando falamos em potências, temos uma base elevada a n, sendo n, portanto, o expoente. Esse número base será multiplicado por si mesmo n vezes. Na radiciação, entretanto, é dada a potência para que seja possível encontrar a base. Nesse processo, nos deparamos com algumas propriedades denominadas propriedades das raízes, ou ainda propriedades dos radicais.
Publicidade
As propriedades dos radicais são aplicadas para que seja mais simples resolver as raízes de índices elevados, ou ainda com um resultado não exato. Precisamos, entretanto, antes de entrar nessa conceituação, lembrar dos radicais. O radical nada mais é do que um símbolo que devemos usar para identificar uma radiciação. Para entendermos melhor, vamos exemplificar abaixo:
![]()
Nesse caso, temos n como o índice, x como o radicando e y como a raíz enésima de x. O símbolo que representa a radiciação é √, sendo denominado radical. Para chegarmos a y, temos que seguir um princípio, seguindo a linha de raciocínio de que y é um número que, ao ser multiplicado por si mesmo n vezes, será igual a x. Disso, podemos tirar que yn = x. Agora podemos seguir os estudos, tendo em mente que a radiciação nada mais é do que o inverso da potenciação.
Propriedades dos radicais
A primeira propriedade dos radicais determina que a raíz enésima de um determinado número elevado a enésima potência, será o próprio número, ou seja, quando o índice for igual ao expoente do radicando, o resultado será igual ao número radicando. Confira:
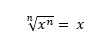
A segunda, por sua vez, afirma que o índice pode ser multiplicado ou dividido por um número qualquer, real, desde que o expoente do radicando seja, também, multiplicado ou dividido pelo mesmo número. A terceira, refere-se ao caso em que as raízes possuem um radicando que é produto de dois números. A raíz enésima do produto, é igual ao produto das raízes enésimas, de forma que podemos representar isso da seguinte maneira:
Publicidade
![]()
A quarta propriedade, faz referência a anterior, porém no que se trata da divisão entre raízes enésimas. Confira:
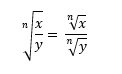
Publicidade
A quinta, por sua vez, refere-se a reescrever a potência de uma raiz, trazendo o expoente para o radicando, conforme demonstrado abaixo:
![]()
A sexta propriedade faz referência às raízes de raízes. Por exemplo, ao considerarmos a raiz enésima da raiz enésima de um determinado número, poderemos reescrever da seguinte forma:
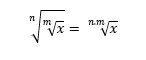
E, por fim, a sétima propriedade trata que quaisquer radicais podem ser escritos na forma de potência com expoente fracionário, conforme demonstrado abaixo:
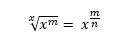
Referências
Matemática – Ensino Médio – Kátia Stocco Smole e Maria Ignez Diniz

Por Natália Petrin
Formada em Publicidade e Propaganda. Atualmente advogada com pós-graduação em Lei Geral de Proteção de Dados e Direito Processual Penal. Mestranda em Criminologia.
Petrin, Natália. Radicais. Todo Estudo. Disponível em: https://www.todoestudo.com.br/matematica/radicais. Acesso em: 04 de February de 2026.

