A geometria espacial é a área da matemática que estuda figuras no espaço, ou seja, que possuem mais de duas dimensões.
Publicidade
Assim como a geometria plana, o estudo da geometria espacial está baseado em axiomas fundamentais. Além dos axiomas já utilizados em geometria plana (ponto, reta e plano), outros quatro são importantes para entender a geometria espacial:
“Por três pontos não colineares passa um único plano”
“Qualquer que seja o plano, existem infinitos pontos nesse plano e infinitos pontos fora dele.”
“Se dois planos distintos têm um ponto em comum, então a intersecção entre eles é uma reta.”
“Se dois pontos de uma reta pertencem a um plano, então essa reta está contida nesse plano.”
(Ferreira et al., 2007, pg.63)
Publicidade
As figuras espaciais que são objeto de estudo desse campo da geometria são conhecidos como sólidos geométricos, ou ainda, figuras geométricas espaciais. Assim, é possível determinar, o volume destes mesmos objetos, ou seja, o espaço que estes ocupam.
Figuras geométricas espaciais
A seguir, alguns dos sólidos geométricos mais conhecidos:
Cubo
Hexaedro regular constituído por 6 faces quadrangulares, 12 arestas e 8 vértices sendo:
Publicidade
Área lateral: 4a2
Área total: 6a2
Volume: a.a.a = a3
Dodecaedro
Poliedro regular com de 12 faces pentagonais, 30 arestas e 20 vértices sendo:
Área Total: 3√25+10√5a2
Volume: 1/4 (15+7√5) a3
Tetraedro
Poliedro regular que apresenta 4 faces triangulares, 6 arestas e 4 vértices sendo:
Área total: 4a2√3/4
Volume: 1/3 Ab.h

Octaedro
Poliedro regular com 8 faces formada por triângulos equiláteros, 12 arestas e 6 vértices sendo:
Área total: 2a2√3
Volume: 1/3 a3√2
Prisma
Poliedro com duas faces paralelas que formam a base. Esta ser triangular, quadrangular, pentagonal, hexagonal. O prisma é composto, além da face, pela altura, lados, vértices e arestas unidos por paralelogramos.
Área da Face: a.h
Área Lateral: 6.a.h
Área da base: 3.a3√3/2
Volume: Ab.h
Onde:
Ab: Área da base
h: altura
Pirâmide
Poliedro que possui uma base, que pode ser triangular, pentagonal, quadrada, retangular, paralelogramo e um vértice que une todas as faces laterais triangulares. Sua altura corresponde a distância entre o vértice e sua base.
Área total: Al + Ab
Volume: 1/3 Ab.h
Onde:
Al: Área lateral
Ab: Área da base
h: altura
Você sabia?
Os “Sólidos Platônicos” são poliedros convexos no quais todas as suas faces são polígonos regulares congruentes formados pelas arestas. Recebem este nome porque Platão foi o primeiro matemático que conseguiu provar a existência de apenas cinco poliedros regulares. No caso, os cinco “sólidos platônicos” são: tetraedro, cubo, octaedro, dodecaedro, icosaedro.
Um poliedro é considerado platônico se obedecer às seguintes condições:
a) for convexo;
b) em todo vértice concorrer o mesmo número de arestas;
c) toda face tiver o mesmo número de arestas;
d) for válida a relação de Euler.
Referências
FERREIRA, E. L. C.; NETO, F. X. F.; RIOS, I. L. Geometria básica. Volume 2, 3ª Edição. Rio de Janeiro : Fundação CECIERJ, 2007.

Por Carlos Ferreira
Formado em Ciências Econômicas e Jornalismo. Possui ampla experiência editorial e redacional em conteúdos jornalísticos com foco em mídias digitais.
Ferreira, Carlos. Geometria Espacial. Todo Estudo. Disponível em: https://www.todoestudo.com.br/matematica/geometria-espacial. Acesso em: 10 de February de 2026.
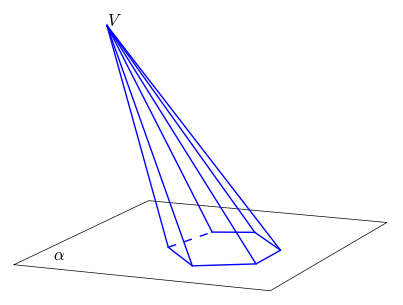
01. [UEM/2008] O sólido S, ilustrado na figura abaixo, foi obtido seccionando-se uma pirâmide não regular, por um plano não paralelo à base da mesma, subtraindo-se a porção que contém o vértice. Com essas considerações, assinale a(s) alternativa(s) correta(s).
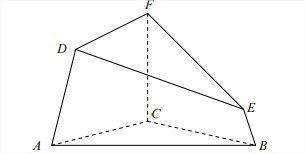
01) Os planos que contêm as faces laterais do sólido S interceptam-se em um ponto.
02) Os planos que contêm as faces ABC e DEF interceptam-se em apenas um ponto.
04) A reta suporte da aresta DF não intercepta o plano que contém a face ABC.
08) Não existe um plano que contenha as retas suportes das arestas AC e DE.
16) A aresta EB é perpendicular a alguma reta do plano que contém a face ABC.
02. [UFBA-2006] Com relação a um prisma reto de base quadrada, é correto afirmar:
01) Cada diagonal de uma face divide-a em dois triângulos congruentes.
02) Existem exatamente 8 segmentos que ligam pares de vértices não pertencentes a uma mesma face.
04) Dadas duas faces não adjacentes e quatro vértices, dois em cada uma dessas faces, existe um plano que contém esses quatro vértices.
08) Dados dois vértices consecutivos, para cada n {1,3,5,7} existe um caminho poligonal que liga esses vértices e é formado por n arestas, cada uma percorrida uma única vez.
16) Se a medida do lado da base e a altura do prisma são números inteiros consecutivos, e o volume é um número primo p, então p é único.
32) Existem exatamente 24 pirâmides distintas cujas bases são faces do prisma e cujos vértices são também vértices do prisma.
01. [Somatório: 24 (08+16=24)]
Comentário:
01) A intersecção de dois planos não coincidentes é uma reta.
02) A intersecção de dois planos não coincidentes é uma reta.
04) Os planos determinados por ABC e DEF não são paralelos. Assim, DF pode ou não interceptar o plano ABC.
02. [somatório 57 (01+08+16+32=57)]