A geometria, um dos ramos da matemática, estuda as figuras geométricas, analisando suas propriedades e medidas no plano. O estudo das figuras planas está diretamente ligado aos conceitos da geometria euclidiana, que surgiu no período da Grécia Antiga. O cálculo relacionado à área das figuras planas geométricas se fez necessário em decorrência da importância disso para a construção das moradias, mas também para plantações.
Publicidade
Tudo surgiu, portanto, de forma bastante intuitiva, nascendo em decorrência da necessidade e da observação humana. Os conhecimentos geométricos, por exemplo, foram necessários para os sacerdotes em tempos antigos, uma vez que deveriam demarcar as terras devastadas pelas enchentes do Rio Nilo e realizar a partilha proporcionalmente ao valor dos impostos pagos. Foi aí que surgiu a necessidade de calcular a área de um determinado espaço.
Foi, entretanto, no ano de 300 a.C. que Euclides de Alexandria desenvolveu trabalhos matemáticos envolvendo a geometria, sendo a sua obra Os Elementos, a maior já publicada do ramo durante toda a história da humanidade.
Figuras Geométricas
Triângulos

Os triângulos são aqueles polígonos que apresentam três lados e três ângulos, e sua área pode ser calculada por meio da multiplicação da base pela altura. Para isso, deve-se tomar por base a ponta do triângulo até a sua base.
Nos triângulos equiláteros, os lados possuem a mesma medida, e para calcular a sua área, podemos usar a fórmula, considerando que b é a base e h é a altura.
Imagem
Quadriláteros
Os quadriláteros são aqueles polígonos que possuem quatro lados. A soma dos ângulos interos, assim como a soma dos ângulos externos, é igual a 360°.
Publicidade

Para os quadrados a o valor da área pode ser encontrado por meio da fórmula abaixo, considerando que l representa o lado.
A = l . l
Para o retângulo, por sua vez, faremos, considerando que c representa comprimento e l a largura:
Publicidade
A = c . l
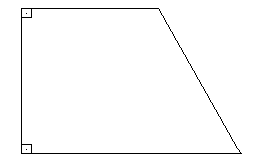
Por sua vez, para o trapézio, devemos usar a fórmula a seguir, considerando que c é a base menor, a é a base maior e h é a altura:
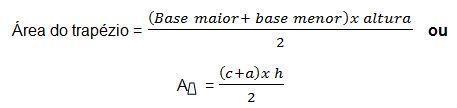
Para o losango, por fim, devemos usar a seguinte fórmula para encontrar sua área, levando em consideração que representa o lado e h a altura:
A = a . h
Círculos

O círculo é um conjunto dos pontos internos de uma circunferência, e sua área pode ser expressa matematicamente por uma fórmula, considerando que r representa o raio da circunferência e π é uma constante:
A = π . r²
Referências
Matemática – Kátia Stocco Smole e Maria Ignez Diniz

Por Natália Petrin
Formada em Publicidade e Propaganda. Atualmente advogada com pós-graduação em Lei Geral de Proteção de Dados e Direito Processual Penal. Mestranda em Criminologia.
Petrin, Natália. Figuras Geométricas (formas geométricas). Todo Estudo. Disponível em: https://www.todoestudo.com.br/matematica/figuras-geometricas. Acesso em: 28 de February de 2026.
01. [PM Pará] Um empresário possui um espaço retangular de 110 m por 90 m para eventos. Considerando que cada metro quadrado é ocupado por 4 pessoas, a capacidade máxima de pessoas que esse espaço pode ter é:
a) 32.400
b) 34.500
c) 39.600
d) 42.500
e) 45.400
02. [PM Pará] Os pontos (2,3), (5,3) e (2,7) são vértices de um triângulo retângulo. A área desse triângulo é:
a) 5 u.a
b) 6 u.a
c) 7 u.a
d) 8 u.a
e) 9 u.a
01. [C]
02. [B]