Velocidade relativa, como o nome diz, é um valor único que representa o movimento relativo entre dois corpos. Dessa maneira, os casos que podem ser estudados com base nesse conceito são para a aproximação e afastamento. Além disso, os movimentos podem estar no mesmo sentido ou sentidos opostos. Continue a leitura para saber mais sobre o assunto.
Publicidade
O que é a velocidade relativa
Velocidade relativa, de maneira geral, é a velocidade de um corpo em relação a outro. Dessa maneira, pode-se classificar o movimento relativo entre dois corpos. Essa classificação pode ser: aproximação e afastamento.
Relacionadas
Por exemplo, imagine que você está viajando de carro. Nessa estrada, quando um carro se aproxima no sentido contrário, o movimento relativo é de aproximação. Além disso, após o encontro, o movimento relativo é o de afastamento.
Velocidade relativa de aproximação
O movimento de aproximação pode acontecer de duas formas. Ou seja, quando os corpos se movimentam no mesmo sentido ou quando estão em sentidos opostos.
Movimento no mesmo sentido
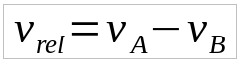
Quando os corpos estão no mesmo sentido, as velocidades são subtraídas. Dessa maneira, a velocidade relativa entre os dois será menor que a velocidade de cada um. Por exemplo, imagine um movimento de aproximação para a ultrapassagem. Se um carro está a 40 km/h e o outro está a 60 km/h a velocidade relativa entre eles é de 20 km/h.
Publicidade
Movimento em sentido oposto
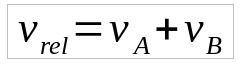
Quando os corpos se movimentam em sentidos opostos, as velocidades são somadas. Assim, a velocidade entre os dois será maior que a velocidade individual. Um exemplo são dois veículos trafegando em uma estrada de pista simples. Ou seja, se um carro está viajando a 80 km/h e o outro está a 90 km/h, a velocidade relativa é 170 km/h.
Note que, para o movimento no mesmo sentido, a velocidade do corpo A deve ser maior que a do corpo B. Entretanto, para o movimento no mesmo sentido, as velocidades são somadas.
Publicidade
Velocidade relativa de afastamento
De maneira similar à aproximação, no movimento de afastamento os corpos podem estar no mesmo sentido ou em sentidos opostos.
Movimento no mesmo sentido
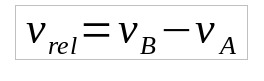
Nesse caso, as velocidades também serão subtraídas. Esse afastamento pode ser entendido como quando o veículo à frente está mais rápido. Por exemplo, o momento após a ultrapassagem.
Movimento em sentido oposto
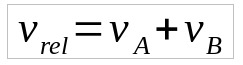
Assim como na aproximação, nesse tipo de movimento, as velocidades serão somadas. Nesse caso, um exemplo é quando dois carros se afastam depois de se cruzarem por uma estrada.
Note que, para a aproximação, a velocidade do corpo B deve ser maior que a do corpo A.
Vídeos sobre velocidade relativa
O conceito de velocidade relativa faz parte da cinemática. Porém, os sinais das velocidades podem confundir algumas pessoas. Dessa forma, selecionamos algumas videoaulas para você aprofundar seus conhecimentos. Veja:
Encontros e ultrapassagens
O professor Marcelo Boaro explica como estudar os casos de encontros e ultrapassagens. Além disso, Boaro também explica que esse estudo deve ser feito apenas quando o movimento for uniforme. Ou seja, quando as velocidades forem constantes. Ao fim da aula, o professor resolve um exercício de aplicação.
Movimento uniforme relativo
O canal Física 2.0 explica como calcular a velocidade relativa em diversos casos. Para isso, o professor conduz a videoaula de maneira dinâmica e descontraída. Ao fim do vídeo, ele resolve um exercício de aplicação.
Como resolver exercícios de encontros e ultrapassagens
Thales, do canal Chama o Físico, explica como resolver exercícios de encontros e ultrapassagens. Esse tipo de exercício é clássico em qualquer prova de física, não é mesmo? Por isso, assista a esse vídeo e não tenha mais medo de resolver sses exercícios.
Para complementar os estudos sobre de física, estude também sobre Movimento Uniforme.
Referências
YOUNG, H. D. et al. Física I: Mecânica. São Paulo: Addison & Wesley. 2016
HALLIDAY, D. et al. Física: Volume 1. Rio de Janeiro: Pearson. 2014

Por Hugo Shigueo Tanaka
Divulgador Científico e co-fundador do canal do YouTube Ciência em Si. Historiador da Ciência. Professor de Física e Matemática. Licenciado em Física pela Universidade Estadual de Maringá (UEM). Mestre em Ensino de Ciências e Matemática (PCM-UEM). Doutorando em Ensino de Ciências e Matemática (PCM-UEM).
Tanaka, Hugo Shigueo. Velocidade Relativa. Todo Estudo. Disponível em: https://www.todoestudo.com.br/fisica/velocidade-relativa. Acesso em: 28 de January de 2026.
1. [PUC]
Um avião em voo horizontal voa a favor do vento com velocidade de 180 Km/h em relação ao solo. Na volta, ao voar contra o vento, o avião voa com velocidade de 150 Km/h em relação ao solo. Sabendo-se que o vento e o módulo da velocidade do avião (em relação ao ar) permanecem constantes, o módulo da velocidade do avião e do vento durante o voo, respectivamente, são:
a) 165 Km/h e 15 Km/h
b) 160 Km/h e 20 Km/h
c) 155 Km/h e 25 Km/h
d) 150 Km/h e 30 Km/h
e) 145 Km/h e 35 Km/h
Alternativa correta: A
Se o avião voa a favor do vento, suas velocidades devem ser somadas:
vavião + vvento = 180 km/h
Contudo, se o voo acontece contra o vento, as velocidades são subtraídas:
vavião – vvento = 150 km/h
Transformando a relação em um sistema e somando os termos:
vavião + vvento = 180 km/h
vavião – vvento = 150 km/h
Obtemos que
2vavião = 330
Logo,
vavião = 165 km/h
Logo, vvento = 15 km/h
2. [Unitau]
Uma motocicleta com velocidade constante de 20 m/s ultrapassa um trem de comprimento 100 m e velocidade 15 m/s. A duração da ultrapassagem é:
a) 5 s
b) 15 s
c) 20 s
d) 25 s
e) 30 s
Alternativa correta: C
Como o movimento dos dois corpos está no mesmo sentido, a velocidade relativa será encontrada a partir da subtração das velocidades.
Assim:
vrel = 20 – 15 = 5 m/s
Sabe-se que a velocidade da moto é em relação ao trem é 5 m/s. Além disso, como o trem tem 100 m de comprimento, encontramos o tempo gasto para a ultrapassagem:
v = Δs/Δt
Δt = 100/5
Δt = 20 s