Ondas estacionárias são figuras de interferência específicas. Dessa forma, quando duas ondas de frequências, comprimentos de onda e amplitudes iguais se encontram, há a formação desse padrão de interferência.
Publicidade
O que são ondas estacionárias?
Ondas estacionárias são aquelas que possuem um padrão de vibração estacionário. Assim, elas se formam a partir da superposição de duas ondas idênticas, que viajam em sentidos opostos. Além disso, esse tipo de fenômeno costuma acontecer quando duas ondas estão confinadas em um espaço.
Exemplos desses fenômenos são as ondas sonoras em um tubo fechado ou ondas em uma corda com duas extremidades fixas. Além disso, como qualquer tipo de onda, as estacionárias possuem comprimento de onda, frequência, período e velocidade de propagação.
Relacionadas
Elementos das ondas estacionárias
Em certas condições, as cordas com extremidades fixas podem gerar ondas estacionárias. Ou seja, ondas idênticas que se sobrepõem. Nesse caso, existem alguns elementos importantes para a descrição desse tipo de movimento ondulatório. Confira:
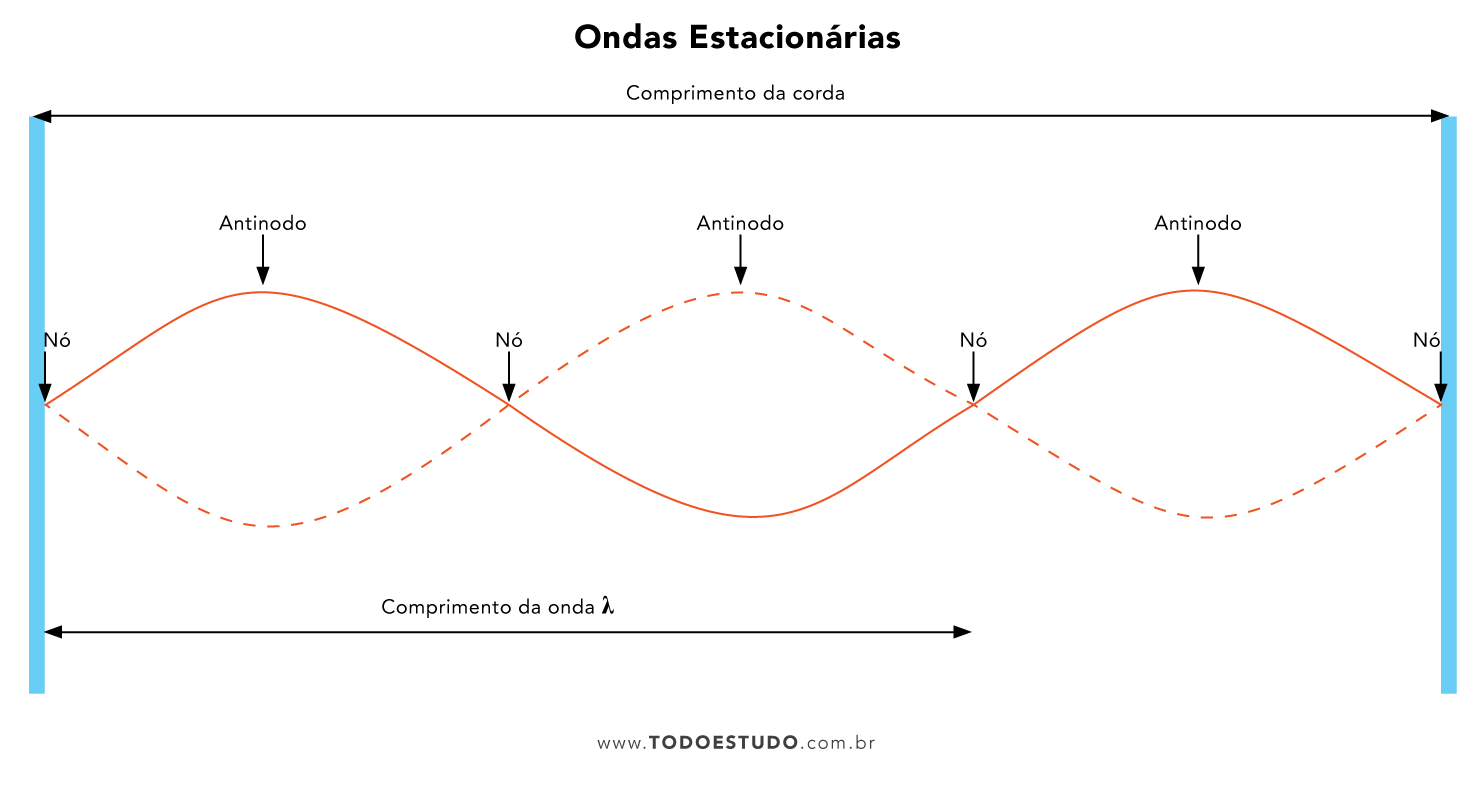
- L: Comprimento da corda.
- Nó: ponto de inflexão entre os pontos de amplitude positiva ou negativa.
- Ventre ou antinodo: Região de máxima amplitude.
- λ: Comprimento de onda.
Além desses elementos, é importante notar que a onda também possui frequência, período e velocidade de propagação. Essas grandezas físicas são descritas a partir de uma análise matemática da onda.
Harmônicos
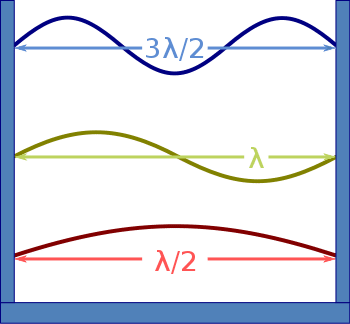
As ondas estacionárias possuem harmônicos. Isso pode acontecer se a onda estiver com as extremidades fixas ou com um das extremidades livres. Por exemplo, se for a corda de um violão ou uma flauta doce, respectivamente.
Publicidade
Primeiro harmônico
O primeiro harmônico possui apenas meio comprimento de onda e é chamado de harmônico fundamental.
Segundo harmônico
O segundo harmônico possui um comprimento de onda completo.
Terceiro harmônico
O terceiro harmônico possui um comprimento de onda e meio (3λ/2).
Publicidade
N-ésimo harmônico
A fim de encontrar qualquer harmônico, pode-se usar a seguinte relação matemática:
![]()
- L: Comprimento da corda (m).
- n: número do harmônico
- λ: Comprimento de onda (m).
Essa relação matemática vale apenas para as ondas estacionárias em uma corda com as extremidades fixas.
Ondas estacionárias e ressonância
Um padrão de ressonância é aquele no qual as ondas vibram em frequências específicas. Dessa maneira, em uma corda com as extremidades fixas, cada frequência de ressonância está associada à formação de ondas estacionárias. A menor frequência de ressonância dá origem ao primeiro harmônico e assim sucessivamente até quantos harmônicos forem possíveis na corda.
Vídeos sobre ondas estacionárias
O estudo da ondulatória pode oscilar entre ser fácil e difícil. Assim, para você compreender o conteúdo, selecionamos alguns vídeos sobre esse tema. Confira:
Ondas em uma corda
Os professores Gil Marques e Claudio Furukawa demonstram experimentalmente como ocorre a formação de uma onda estacionária. Além disso, o experimento feito no vídeo pode ser facilmente reproduzido para feiras de ciências.
O que é o harmônico fundamental
Muito se fala sobre os harmônicos em uma corda. Contudo, não se fala muito como calculá-los. Para isso, o professor Thales, do canal Chama o Físico, explica como encontrar o primeiro harmônico. Isto é, o harmônico fundamental.
Cordas vibrantes
O professor Marcelo Boaro explica como estudar as cordas vibrantes. Esse tipo de fenômeno físico faz parte do conteúdo de ondulatória. Além disso, ao final do vídeo, Boaro resolve um exercício de aplicação para te ajudar no entendimento do assunto.
As ondas estacionárias podem ser descritas como sendo ondas eletromagnéticas. Aproveite seus estudos de física e aprenda mais sobre as ondas mecânicas.
Referências
YOUNG, H. D et al. Física II: Termodinâmica e ondas. São Paulo: Addison & Wesley. 2016
HALLIDAY, D. et al. Fundamentos de Física II: Gravitação, ondas e termodinâmica. Rio de Janeiro: Pearson. 2008.

Por Hugo Shigueo Tanaka
Divulgador Científico e co-fundador do canal do YouTube Ciência em Si. Historiador da Ciência. Professor de Física e Matemática. Licenciado em Física pela Universidade Estadual de Maringá (UEM). Mestre em Ensino de Ciências e Matemática (PCM-UEM). Doutorando em Ensino de Ciências e Matemática (PCM-UEM).
Tanaka, Hugo Shigueo. Ondas estacionárias. Todo Estudo. Disponível em: https://www.todoestudo.com.br/fisica/ondas-estacionarias. Acesso em: 04 de February de 2026.
1. [Uece]
Para uma corda de piano de comprimento L, as possíveis ondas estacionárias de menor frequência têm comprimentos de onda iguais a:

Alternativa correta: C
Dos harmônicos, têm se:
Primeiro harmônico: λ = 2L.
Segundo harmônico: λ = L.
Terceiro harmônico: λ = 2L/3.
2. [Enem]
Em um violão afinado, quando se toca a corda Lá com seu comprimento efetivo (harmônico fundamental), o som produzido tem frequência de 440 Hz. Se a mesma corda do violão é comprimida na metade do seu comprimento, a frequência do novo harmônico:
a) se reduz à metade, porque o comprimento de onda dobrou.
b) dobra, porque o comprimento de onda foi reduzido à metade.
c) quadruplica, porque o comprimento de onda foi reduzido à metade.
d) quadruplica, porque o comprimento de onda foi reduzido à quarta parte.
e) não se modifica, porque é uma característica independente do comprimento da corda que vibra.
Alternativa correta: B
Como a velocidade de propagação é constante, não dependendo da
ordem do harmônico, se o comprimento da corda é reduzido à metade, o comprimento de onda também se reduz à metade, dobrando a frequência do harmônico fundamental.